
【題目】閱讀下面材料:
在數學課上,老師請同學思考如下問題:
請利用直尺和圓規確定圓中弧AB所在圓的圓心![]()
小亮的作法如下:
如圖:
① 在弧AB上任意取一點C,分別連接AC,BC
②分別作AC,BC的垂直平分線,兩條垂線平分線交于O點,所以點O就是所求弧AB的圓心
老師說:“小亮的作法正確.”
請你回答:小亮的作圖依據是 .
科目:初中數學 來源: 題型:
【題目】“圓材埋壁”是我國古代著名數學著作《九章算術》中的一個問題:“今有圓材,埋在壁中,不知大小,以鋸鋸之,深一寸,鋸道長一尺,問徑幾何”此問題的實質就是解決下面的問題:“如圖,CD為⊙O的直徑,弦AB⊥CD于點E,CE=1,AB=10,求CD的長”.根據題意可得CD的長為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,P、Q分別是BC、AC上的點,作PR⊥AB,PS⊥AC,垂足分別為R、S,若AQ=PQ,PR=PS,則結論:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正確的有( )

A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
情境再現:
舉世矚目的港珠澳大橋東接香港,西接珠海、澳門,全長![]() 千米,是世界上最長的跨海大橋,被譽為“新世界七大奇跡”之一.如圖,香港口岸點
千米,是世界上最長的跨海大橋,被譽為“新世界七大奇跡”之一.如圖,香港口岸點![]() 至珠海口岸點
至珠海口岸點![]() 約
約![]() 千米,海底隧道
千米,海底隧道![]() 全長約
全長約![]() 千米,隧道一端的東人工島點
千米,隧道一端的東人工島點![]() 到香港口岸的路程為
到香港口岸的路程為![]() 千米.某一時刻,一輛穿梭巴士從香港口岸發車,沿港珠澳大橋開往珠海口岸.
千米.某一時刻,一輛穿梭巴士從香港口岸發車,沿港珠澳大橋開往珠海口岸.![]() 分鐘后,一輛私家車也從香港口岸出發沿港珠澳大橋開往珠海口岸.在私家車出發的同時,一輛大客車從珠海口岸出發開往香港口岸.已知穿梭巴士的平均速度為
分鐘后,一輛私家車也從香港口岸出發沿港珠澳大橋開往珠海口岸.在私家車出發的同時,一輛大客車從珠海口岸出發開往香港口岸.已知穿梭巴士的平均速度為![]() 千米/時,大客車的平均速度為
千米/時,大客車的平均速度為![]() 千米/時,私家車的平均速度為
千米/時,私家車的平均速度為![]() 千米/時.
千米/時.
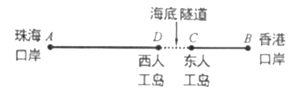
問題解決:
(1)穿梭巴士出發多長時間與大客車相遇?
(2)私家車能否在到達珠海口岸前追上穿梭巴士?說明理由;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段AD上一點,點B為CD的中點,且AD=8 cm,BD=2 cm.
(1)圖中共有多少條線段?
(2)求AC的長.
(3)若點E在直線AD上,且EA=3 cm,求BE的長.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC三個頂點的坐標為A(1,2),B(4,1),C(2,4).
(1)在圖中畫出△ABC關于y軸對稱的圖形△A’B’C’;
(2)在圖中x軸上作出一點P,使PA+PB的值最小;并寫出點P的坐標.
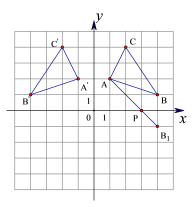
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC是直角三角形,∠C=90°,∠CAB的角平分線AE與 AB的垂直平分線DE相交于點E.
(1)如圖2,若點E正好落在邊BC上.
①求∠B的度數
②證明:BC=3DE
(2)如圖3,若點E滿足C、E、D共線.
求證:AD+DE=BC.
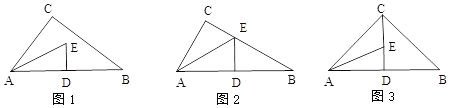
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把一個長方形的紙片對折兩次,然后剪下一個角,為了得到一個鈍角為100° 的菱形,剪口與折痕所成的角的度數應為( )
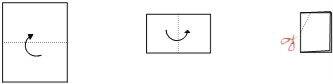
A. 25°或50° B. 20°或50° C. 40°或50° D. 40°或80°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系 ![]() 中,正比例函數
中,正比例函數 ![]() 與反比例函數
與反比例函數 ![]() 的圖象交于A,B兩點,點A的橫坐標為2,AC⊥x軸于點C,連接BC.
的圖象交于A,B兩點,點A的橫坐標為2,AC⊥x軸于點C,連接BC.
(1)求反比例函數的表達式;
(2)若點P是反比例函數 ![]() 圖象上的一點,且滿足△OPC的面積是△ABC面積的一半,請直接寫出點P的坐標.
圖象上的一點,且滿足△OPC的面積是△ABC面積的一半,請直接寫出點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com