
【題目】如圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 相交于點
相交于點![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)在![]() 軸上一點
軸上一點![]() ,若
,若![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)直線![]() 上一點
上一點![]() ,平面內一點
,平面內一點![]() ,若以
,若以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 全等,求點
全等,求點![]() 的坐標.
的坐標.
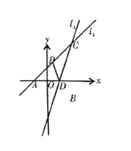
【答案】(1)![]() ;(2)點
;(2)點![]() 坐標為
坐標為![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)令![]() 中y=0即可求得答案;
中y=0即可求得答案;
(2)點![]() 在
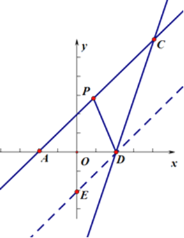
在![]() 的下方,過點D作DE∥AC交y軸于E,求出DE的解析式即可得到點E的坐標,利用對稱性即可得到點E在AC上方時點E的坐標;
的下方,過點D作DE∥AC交y軸于E,求出DE的解析式即可得到點E的坐標,利用對稱性即可得到點E在AC上方時點E的坐標;
(3)求出直線與x軸的夾角度數,線段AD的長度,分三種情況求出點F的坐標.
(1)∵點![]() 是
是![]() 與
與![]() 軸的交點,
軸的交點,![]() 代入
代入![]() ,
,![]() ,
,
∴點![]() 的坐標
的坐標![]() ;
;
(2)當點![]() 在
在![]() 的下方,過點
的下方,過點![]() 作
作![]() ,交
,交![]() 軸于點
軸于點![]() ,
,
設![]() 解析式為
解析式為![]() ,過
,過![]() ,
,
∴2+b=0,得b=-2,
∴![]() ,
,
∴![]() ,
,
點![]() 在
在![]() 上方,同理可得
上方,同理可得![]() ,
,
綜上:點![]() 坐標為
坐標為![]() 或
或![]()
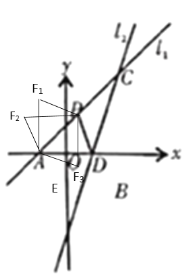
(3)直線![]() 與x軸的夾角是45
與x軸的夾角是45![]() ,
,
∵A(-2,0),D(2,0),
∴AD=4,
作AF1⊥x軸,當A1F=AD=4時,△AF1P≌△ADP,此時點F1的坐標是(-2,4);
作PF2∥AD,當F2=AD=4時,△APF2≌△PAD,此時點F2的坐標是(-3,3);
作PF3⊥x軸,當PF3=AD=4時,△APF3≌△PAD,此時點F3的坐標是(1,-1),
綜上,點F的坐標為 ![]() .
.


 小題狂做系列答案
小題狂做系列答案科目:初中數學 來源: 題型:
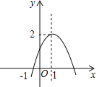
【題目】如圖,已知二次函數![]() 圖象過點
圖象過點![]() ,頂點為
,頂點為![]() ,則結論:①
,則結論:①![]() ;②
;②![]() 時,函數的最大值是
時,函數的最大值是![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正確的結論有( )
.其中正確的結論有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
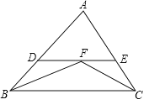
【題目】如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點F,點點F作DE∥BC,交AB于點D,交AC于點E。若BD=3,DE=5,則線段EC的長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在正方形ABCD外取一點E,連接AE、BE、DE.過點A作AE的垂線交DE于點P.若AE=AP=1,PB=![]() .下列結論:①△APD≌△AEB;②點B到直線AE的距離為
.下列結論:①△APD≌△AEB;②點B到直線AE的距離為![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正確結論的序號是( )
.其中正確結論的序號是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
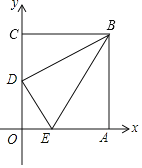
【題目】如圖,在平面直角坐標系中,長方形OABC的頂點O在坐標原點,頂點A、C分別在x、y軸的正半軸上:OA=3,OC=4,D為OC邊的中點,E是OA邊上的一個動點,當△BDE的周長最小時,E點坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】快車和慢車都從甲地駛向乙地,兩車同時出發行在同一條公路上,途中快車休息1小時后加速行駛比慢車提前0.5小時到達目的地,慢車沒有體息整個行駛過程中保持勻速不變.設慢車行駛的時間為x小時,快車行駛的路程為y1千米,慢車行駛的路程為y2千米,圖中折線OAEC表示y1與x之間的函數關系,線段OD表示y2與x之間的函數關系,請解答下列問題:
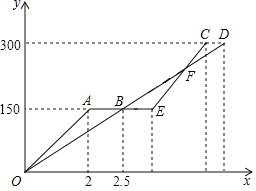
(1)甲、乙兩地相距 千米,快車休息前的速度是 千米/時、慢車的速度是 千米/時;
(2)求圖中線段EC所表示的y1與x之間的函數表達式;
(3)線段OD與線段EC相交于點F,直接寫出點F的坐標,并解釋點F的實際意義.
查看答案和解析>>
科目:初中數學 來源: 題型:
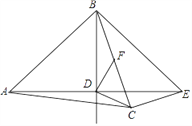
【題目】如圖,在△ABC中,AB=AC,點D是△ABC內一點,AD=BD,且AD⊥BD,連接CD.過點C作CE⊥BC交AD的延長線于點 E,連接BE.過點D作DF⊥CD交BC于點F.
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的長;
,求BC的長;
(2)若BD=DE,求證:BF=CF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖像分別與
的圖像分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() ,以線段
,以線段![]() 為邊在第四象限內作等腰直角
為邊在第四象限內作等腰直角![]() ,且
,且![]() .
.
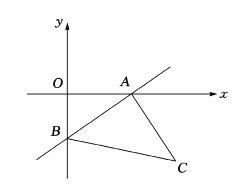
(1)試寫出點![]() 的坐標:
的坐標: ![]() (_ _,_ ___),
(_ _,_ ___),![]() (_ ,_ )
(_ ,_ )
(2)求點![]() 的坐標;
的坐標;
(3)求直線![]() 的函數表達式
的函數表達式
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com