
【題目】在△ABC中,∠BAC=90°,AB=AC,點D為直線BC上一動點(點D不與B、C重合),以AD為直角邊在AD右側作等腰直角三角形ADE,且∠DAE=90°,連接CE.

(1)如圖①,當點D在線段BC上時:
①BC與CE的位置關系為 ;
②BC、CD、CE之間的數量關系為 .
(2)如圖②,當點D在線段CB的延長線上時,結論①,②是否仍然成立?若不成立,請你寫出正確結論,并給予證明.
(3)如圖③,當點D在線段BC的延長線上時,BC、CD、CE之間的數量關系為 .
【答案】(1)①BC⊥CE;②BC=CD+CE;(2)結論①成立,②不成立,結論:CD=BC+CE;(3)CE=BC+CD.
【解析】
(1)①利用條件求出△ABD≌△ACE,隨之即可得出位置關系.
②根據BD=CE,可得BC=BD+CD=CE+CD.
(2)根據第二問的條件得出△ABD≌△ACE,隨之即可證明結論是否成立.
(3)分析新的位置關系得出△ABD≌△ACE,即可得出CE=BC+CD.
(1)如圖1.
∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE.在△ABD和△ACE中,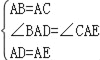 ,∴△ABD≌△ACE(SAS),∴BD=CE,∠B=∠ACE=45°,①∵∠ACE=45°=∠ACB,∴∠BCE=45°+45°=90°,即BD⊥CE;
,∴△ABD≌△ACE(SAS),∴BD=CE,∠B=∠ACE=45°,①∵∠ACE=45°=∠ACB,∴∠BCE=45°+45°=90°,即BD⊥CE;
②∵BD=CE,∴BC=BD+CD=CE+CD.
故答案為:BC⊥CE,BC=CD+CE;
(2)結論①成立,②不成立,結論:CD=BC+CE
理由:如圖2中,∵∠BAC=∠DAE=90°,∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,即∠BAD=∠EAC.在△ABD和△ACE中,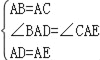 ,∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABD=135°,∴CD=BC+BD=BC+CE
,∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABD=135°,∴CD=BC+BD=BC+CE
∵∠ACB=45°
∴∠DCE=90°,∴CE⊥BC;
(3)如圖3中,∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD
即∠BAD=∠CAE,∴在△ABD和△ACE中,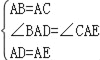 ,∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABC.
,∴△ABD≌△ACE(SAS),∴BD=CE,∠ACE=∠ABC.
∵AB=AC,∴∠ABC=∠ACB=45°,∴BD=BC+CD,即CE=BC+CD.
故答案為:CE=BC+CD.


科目:初中數學 來源: 題型:
【題目】下面說法正確的是個數有( )
①如果三角形三個內角的比是1:2:3,那么這個三角形是直角三角形;
②如果三角形的一個外角等于與它相鄰的一個內角,則這么三角形是直角三角形;
③如果一個三角形的三條高的交點恰好是三角形的一個頂點,那么這個三角形是直角三角形;
④如果∠A=∠B=![]() ∠C,那么△ABC是直角三角形;
∠C,那么△ABC是直角三角形;
⑤若三角形的一個內角等于另兩個內角之差,那么這個三角形是直角三角形;
⑥在△ABC中,若∠A+∠B=∠C,則此三角形是直角三角形.
A.3個 B.4個 C.5個 D.6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了解七年級男生體質健康情況,隨機抽取若干名男生進行測試,測試結果分為優秀、良好、合格、不合格四個等級,統計整理數據并繪制圖1、圖2兩幅不完整的統計圖,請根據圖中信息回答下列問題: 
(1)本次接收隨機抽樣調查的男生人數為人,扇形統計圖中“良好”所對應的圓心角的度數為;
(2)補全條形統計圖中“優秀”的空缺部分;
(3)若該校七年級共有男生480人,請估計全年級男生體質健康狀況達到“良好”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據下圖回答問題:
(1)上圖表示的是哪兩個變量之間的關系?哪個是自變量,哪個是因變量?
(2)從圖象中觀察,哪一年的居民的消費價格最低?哪一年居民的消費價格最高?相差多少?
(3)哪些年的居民消費價格指數與1989年的相當?
(4)圖中A點表示什么?
(5)你能夠大致地描述1986—2000年價格指數的變化情況嗎?試試看.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校籃球社團決定購買運動裝備。經了解,甲、乙兩家運動產品經銷店以同樣的價格出售某種品牌的隊服和籃球,已知每套隊服比每個籃球多![]() 元,兩套隊服與三個籃球的費用相等.經洽談,甲店的優惠方案是:每購買十套隊服,送一個籃球,乙店的優惠方案是:若購買隊服超過
元,兩套隊服與三個籃球的費用相等.經洽談,甲店的優惠方案是:每購買十套隊服,送一個籃球,乙店的優惠方案是:若購買隊服超過![]() 套,則購買籃球打八折.
套,則購買籃球打八折.
(1)求每套隊服和每個籃球的價格是多少?
(2)若籃球社團購買![]() 套隊服和
套隊服和![]() 個籃球(
個籃球(![]() 是大于
是大于![]() 的整數),請用含
的整數),請用含![]() 的式子分別表示出到甲經銷店和乙經銷店購買裝備所花的費用;
的式子分別表示出到甲經銷店和乙經銷店購買裝備所花的費用;
(3)在(2)的條件下,若![]() ,通過計算判斷到甲、乙哪家經銷店購買更劃算。
,通過計算判斷到甲、乙哪家經銷店購買更劃算。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中考英語聽力測試期間T需要杜絕考點周圍的噪音.如圖,點A是某市一中考考點,在位于考點南偏西15°方向距離500米的C點處有一消防隊.在聽力考試期間,消防隊突然接到報警電話,消防車需沿北偏東75°方向的公路CF前往救援.已知消防車的警報聲傳播半徑為400米,若消防車的警報聲對聽力測試造成影響,則消防車必須改道行駛.試問:消防車是否需要改道行駛?
說明理由.( ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖 1,是一個長為 2m,寬為 2n 的長方形,沿圖中虛線用剪刀將其均分成四個完全相同的小長方形,然后按圖 2 的形狀拼圖.
(1)圖 2 中的圖形陰影部分的邊長為 ;(用含 m、n 的代數式表示)
(2)請你用兩種不同的方法分別求圖 2 中陰影部分的面積; 方法一: ;方法二: .
(3)觀察圖 2,請寫出代數式(m+n)2、(m﹣n)2、4mn 之間的關系式: .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某車間每天可以生產甲種零件600個或乙種零件300個或丙種零件500個,這三種零件各一個可以配成一套,現在要用63天的生產中,使生產的三中零件全部配套,這個車間應該對這三種零件的生產各用幾天才能生產出來的零件配套.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們約定:如果身高在選定標準的±2%范圍之內都稱為“普通身高”.為了了解某校九年級男生中具有“普遍身高”的人數,我們從該校九年級男生中隨機抽出10名男生,分別測量出他們的身高(單位:cm),收集并整理如下統計表:

(1)計算這組數據的三個統計量:平均數、中位數、眾數;
(2)請你選擇其中一個統計量作為選定標準,找出這10名男生中具有“普遍身高”是哪幾位男生?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com