
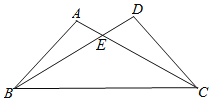
【題目】(本小題滿分8分)如圖,已知∠A=∠D,有下列五個條件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能證明△ABC與△DCB全等的條件有幾個?并選擇其中一個進行證明.
【答案】見解析
【解析】共5個:①或②或③或④或⑤.
若選①AE=DE,則證明如下:
在△ABE和△DCE中, ,
,
∴AB=DC,BE=CE,∴DE+BE=AE+CE,∴BD=AC,
在△ABC和△DCB中, ,∴△ABC≌△DCB(SSS);(2分)
,∴△ABC≌△DCB(SSS);(2分)
若選②BE=CE,則證明如下:
∵BE=CE,∴∠EBC=∠ECB,
在△ABC與△DCB中, ,∴△ABC≌△DCB(AAS);(3分)
,∴△ABC≌△DCB(AAS);(3分)
若選③AB=DC,則證明如下:
在△ABE和△DCE中, ,∴△ABE≌△DCE(AAS),
,∴△ABE≌△DCE(AAS),
∴BE=CE,∴∠EBC=∠ECB,
在△ABC與△DCB中, ,∴△ABC≌△DCB(AAS);(5分)
,∴△ABC≌△DCB(AAS);(5分)
若選④∠ABC=∠DCB,則證明如下:
在△ABC與△DCB中, ,∴△ABC≌△DCB(AAS);(6分)
,∴△ABC≌△DCB(AAS);(6分)
若選⑤AC=BD,則證明如下:
如圖,延長BA,CD交于點F,

∵∠BAC=∠CDB,∴∠FAC=∠FDB,
又∵∠F=∠F,BD=CA,∴△BDF≌△CAF,
∴BF=CF,AF=DF,∴AB=CD,
在△ABE和△DCE中, ,
,
∴△ABE≌△DCE(AAS),
∴BE=CE,∴∠EBC=∠ECB,
在△ABC與△DCB中, ,
,
∴△ABC≌△DCB(AAS).
綜上所述,能證明△ABC與△DCB全等的條件有5個.(8分)


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
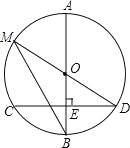
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點E,且CD=24,點M在⊙O上,MD經過圓心O,聯結MB.
(1)若BE=8,求⊙O的半徑;
(2)若∠DMB=∠D,求線段OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,用量角器度量幾個角的度數,下列結論中正確的是( )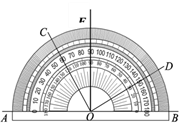
A.∠BOC=60°
B.∠COA是∠EOD 的余角
C.∠AOC=∠BOD
D.∠AOD與∠COE互補
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】截止到2019年2月19日,浙江省的注冊志愿者人數達到14 480 000人. 數據14 480 000用科學記數法表示為( )
A.1.4487B.1448×104C.14.48×106D.1.448×107
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出下列說法:①0是整數;②-3.5是負分數;③5.4不是正數;④自然數一定是正數;⑤負分數一定是負有理數,其中正確的有( ).
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com