
【題目】已知二次函數![]() 圖象如圖所示,對稱軸為過點
圖象如圖所示,對稱軸為過點![]() 且平行于
且平行于![]() 軸的直線,則下列結論中正確的是( )
軸的直線,則下列結論中正確的是( )
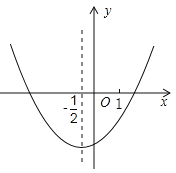
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由拋物線開口向上,與y軸交于負半軸,對稱軸在y軸左側即可判斷a、c、b的符號,進而可判斷A項;
拋物線的對稱軸為直線x=﹣![]() ,結合拋物線的對稱軸公式即可判斷B項;
,結合拋物線的對稱軸公式即可判斷B項;
由圖象可知;當x=1時,a+b+c<0,再結合B項的結論即可判斷C項;
由(1,0)與(﹣2,0)關于拋物線的對稱軸對稱,可知當x=-2時,y<0,進而可判斷D項.
解:A、∵拋物線開口向上,與y軸交于負半軸,對稱軸在y軸左側,∴a>0,c<0,![]() <0,∴b>0,∴abc<0,所以本選項錯誤;
<0,∴b>0,∴abc<0,所以本選項錯誤;
B、∵拋物線的對稱軸為直線x=﹣![]() ,∴
,∴![]() ,∴a﹣b=0,所以本選項錯誤;
,∴a﹣b=0,所以本選項錯誤;
C、∵當x=1時,a+b+c<0,且a=b,∴![]() ,所以本選項錯誤;
,所以本選項錯誤;
D、∵(1,0)與(﹣2,0)關于拋物線的對稱軸對稱,且當x=1時,y<0,∴當x=-2時,y<0,即4a﹣2b+c<0,∴![]() ,所以本選項正確.
,所以本選項正確.
故選:D.


科目:初中數學 來源: 題型:
【題目】如下圖,在△ABC中,∠ACB=90°,D是AB的中點,以DC為直徑的⊙O交△ABC的邊于G,F,E點.求證:(1)∠A=∠GEF;(2)△BDF≌FEC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某化工材料經銷商購進一種化工材料若干千克,成本為每千克30元,物價部門規定其銷售單價不低于成本價且不高于成本價的2倍,經試銷發現,日銷售量![]() (千克)與銷售單價
(千克)與銷售單價![]() (元)符合一次函數關系,如圖所示.
(元)符合一次函數關系,如圖所示.
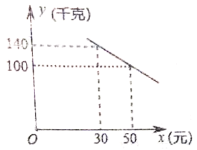
(1)求![]() 與
與![]() 之間的函數關系式,并寫出自變量
之間的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(2)若在銷售過程中每天還要支付其他費用500元,當銷售單價為多少時,該公司日獲利最大?最大獲利是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下圖顯示了用計算機模擬隨機拋擲一枚硬幣的某次實驗的結果
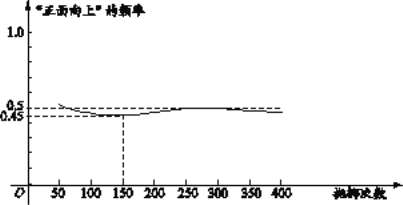
下面有三個推斷:
①當拋擲次數是100時,計算機記錄“正面向上”的次數是47,所以“正面向上”的概率是0.47;
②隨著試驗次數的增加,“正面向上”的頻率總在0.5附近擺動,顯示出一定的穩定性,可以估計“正面向上”的概率是0.5;
③若再次用計算機模擬此實驗,則當拋擲次數為150時,“正面向上”的頻率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中數學 來源: 題型:
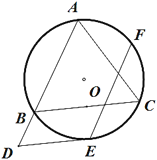
【題目】如圖,△ABC內接于⊙O,AB=AC=10,BC=12,點E是弧BC的中點.
(1)過點E作BC的平行線交AB的延長線于點D,求證:DE是⊙O的切線.
(2)點F是弧AC的中點,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有![]() 、
、![]() 兩個不透明的盒子,
兩個不透明的盒子,![]() 盒中裝有紅色、黃色、藍色卡片各1張,
盒中裝有紅色、黃色、藍色卡片各1張,![]() 盒中裝有紅色、黃色卡片各1張,這些卡片除顏色外都相同.現分別從
盒中裝有紅色、黃色卡片各1張,這些卡片除顏色外都相同.現分別從![]() 、
、![]() 兩個盒子中任意摸出一張卡片.
兩個盒子中任意摸出一張卡片.
(1)從![]() 盒中摸出紅色卡片的概率為______;
盒中摸出紅色卡片的概率為______;
(2)用畫樹狀圖或列表的方法,求摸出的兩張卡片中至少有一張紅色卡片的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
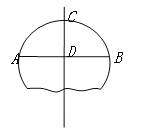
【題目】如圖,破殘的圓形輪片上,弦AB的垂直平分線交AB于C,交弦AB于D.
(1)求作此殘片所在的圓(不寫作法,保留作圖痕跡);
(2)若AB=24cm,CD=8cm,求(1)中所作圓的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】樂至縣城有兩座遠近聞名的南北古塔,清朝道光11年至13年(公元1831--1833年)修建,南塔名為“文運塔”,高30米;北塔名為“凌云塔”.為了測量北塔的高度AB,身高為1.65米的小明在C處用測角儀CD,(如圖所示)測得塔頂A的仰角為45°,此時小明在太陽光線下的影長為1.1米,測角儀的影長為1米.隨后,他再向北塔方向前進14米到達H處,又測得北塔的頂端A的仰角為60°,求北塔AB的高度.(參考數據![]() ≈1.414,
≈1.414,![]() ≈1.732,結果保留整數)
≈1.732,結果保留整數)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“綠水青山就是金山銀山”的理念已融入人們的日常生活中,因此,越來越多的人喜歡騎自行車出行,某自行車店在銷售某型號自行車時,以高出進價的50%標價.已知按標價九折銷售該型號自行車8輛與將標價直降100元銷售7輛獲利相同.
(1)求該型號自行車的進價和標價分別是多少元?
(2)若該型號自行車的進價不變,按(1)中的標價出售,該店平均每月可售出50輛;若每輛自行車每降價20元,每月可多售出5輛,求該型號自行車降價多少元時,每月可獲利30000元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com