
【題目】如圖,∠ABC=∠ACB,AD、BD、CD分別平分△ABC的外角∠EAC、內角∠ABC、外角∠ACF.以下結論:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正確的結論的有__________.(把正確結論的序號都寫上去)

【答案】①②③
【解析】
根據角平分線定義得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根據三角形的內角和定理得出∠BAC+∠ABC+∠ACB=180°,根據三角形外角性質得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,結合題中所給結論逐步推理,即可判斷各項.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正確;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC,
∴∠ACB=2∠ADB,∴②正確;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=![]() ∠EAC,∠DCA=
∠EAC,∠DCA=![]() ∠ACF,
∠ACF,
∵∠EAC=∠ACB+∠ABC,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°(∠DAC+∠ACD)
=180°![]() (∠EAC+∠ACF)
(∠EAC+∠ACF)
=180°![]() (∠ABC+∠ACB+∠ABC+∠BAC)
(∠ABC+∠ACB+∠ABC+∠BAC)
=180°![]() (180°+∠ABC)
(180°+∠ABC)
=90°![]() ∠ABC
∠ABC
=90°﹣∠ABD,∴③正確;
∵∠ACF=2∠DCF,∠ACF=∠BAC+∠ABC,∠ABC=2∠DBC,∠DCF=∠DBC+∠BDC,
∴∠BAC=2∠BDC,∴④錯誤;
故答案為:①②③.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,已知平面直角坐標系內A(2a-1,4),B(-3,3b+1),A、B兩點關于y軸對稱。
(1)求A、B的坐標
(2)動點P、Q分別從A點、B點同時出發,沿直線AB向右運動,同向而行,P點的速度是每秒2個單位長度,Q點的速度是每秒4個單位長度,設P、Q的運動時間為t秒,當0<t<3時.
①請用含t的代數式表示三角形OPQ的面積S,
②在平面直角坐標系中存在一點M,點M的橫縱坐標相等,且滿足![]() ,求出點M的坐標,并求出當
,求出點M的坐標,并求出當![]() =15時,三角形OPQ的面積.
=15時,三角形OPQ的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知B港口位于A觀測點北偏東53.2°方向,且其到A觀測點正北方向的距離BD的長為16km,一艘貨輪從B港口以40km/h的速度沿如圖所示的BC方向航行,15min后達到C處,現測得C處位于A觀測點北偏東79.8°方向,求此時貨輪與A觀測點之間的距離AC的長(精確到0.1km).(參考數據:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學準備購買筆和本子送給農村希望小學的同學,在市場上了解到某種本子的單價比某種筆的單價少4元,且用30元買這種本子的數量與用50元買這種筆的數量相同.
(1)求這種筆和本子的單價;
(2)該同學打算用自己的100元壓歲錢購買這種筆和本子,計劃100元剛好用完,并且筆和本子都買,請列出所有購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點(-1,y1),(2,y2),(3,y3)在反比例函數![]() 的圖象上.下列結論中正確的是( )
的圖象上.下列結論中正確的是( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y1>y2 D. y2>y3>y1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】江南農場收割小麥,已知1臺大型收割機和3臺小型收割機1小時可以收割小麥1.4公頃,2臺大型收割機和5臺小型收割機1小時可以收割小麥2.5公頃.
(1)每臺大型收割機和每臺小型收割機1小時收割小麥各多少公頃?
(2)大型收割機每小時費用為300元,小型收割機每小時費用為200元,兩種型號的收割機一共有10臺,要求2小時完成8公頃小麥的收割任務,且總費用不超過5400元,有幾種方案?請指出費用最低的一種方案,并求出相應的費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某檢修小組乘一輛檢修車沿鐵路檢修,規定向東走為正,向西走為負,該小組的出發地記為A,某天檢修完畢時,行走記錄(單位.千米)如下.
+10,-2,+3,-1,+5,-3,-2,+11,+3,-4,+6.
(1)問收工時,檢修小組距出發地有多遠?在東側還是西側?
(2)距離A最近的一次是哪一次?距離多遠?
(3)若檢修車每千米耗油2.8升,求從出發到收工共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
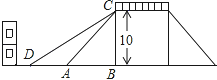
【題目】如圖是一座人行天橋的示意圖,天橋的高度是10米,CB⊥DB,坡面AC的傾斜角為45°.為了方便行人推車過天橋,市政部門決定降低坡度,使新坡面DC的坡度為i=![]() :3.若新坡角下需留3米寬的人行道,問離原坡角(A點處)10米的建筑物是否需要拆除?(參考數據:
:3.若新坡角下需留3米寬的人行道,問離原坡角(A點處)10米的建筑物是否需要拆除?(參考數據: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線![]() 的頂點為A.
的頂點為A.
(1)求點A的坐標;

(2)將線段![]() 沿
沿![]() 軸向右平移2個單位得到線段
軸向右平移2個單位得到線段![]() .
.
①直接寫出點![]() 和
和![]() 的坐標;
的坐標;
②若拋物線![]() 與四邊形
與四邊形![]() 有且只有兩個公共點,結合函數的圖象,求
有且只有兩個公共點,結合函數的圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com