
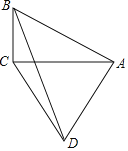
【題目】如圖,AC,BD為四邊形ABCD的對角線,AC⊥BC,AB⊥AD,CA=CD.若tan∠BAC=![]() .則tan∠DBC的值是( )
.則tan∠DBC的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根據tan∠BAC=![]() ,得出∠BAC的度數,則在Rt△ACB中,設BC=1,則AC=
,得出∠BAC的度數,則在Rt△ACB中,設BC=1,則AC=![]() ;證明△CAD為等邊三角形,過點D作DE⊥CA,交CA于點E,設CA與BD交于點F,則DE∥BC,從而∠DBC=∠FDE,設CF=x,則EF=
;證明△CAD為等邊三角形,過點D作DE⊥CA,交CA于點E,設CA與BD交于點F,則DE∥BC,從而∠DBC=∠FDE,設CF=x,則EF=![]() ﹣x,根據tan∠DBC=tan∠FDE列出關于x的方程,解得x值,則可求得tan∠DBC的值.
﹣x,根據tan∠DBC=tan∠FDE列出關于x的方程,解得x值,則可求得tan∠DBC的值.
∵tan∠BAC=![]() ,
,
∴∠BAC=30°,
∵AC⊥BC,
∴∠ACB=90°,
∴設BC=1,則AC=![]() ,
,
∵AB⊥AD,
∴∠BAD=90°,
∴∠DAC=60°,
∵CA=CD,
∴△CAD為等邊三角形,
過點D作DE⊥CA,交CA于點E,設CA與BD交于點F,如圖,
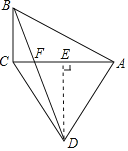
則有:CE=![]() AC=
AC=![]() ,DE=ADsin60°=
,DE=ADsin60°=![]() ×
×![]() =
=![]() ,
,
設CF=x,則EF=![]() ﹣x,
﹣x,
∵AC⊥BC,DE⊥CA,
∴DE∥BC,
∴∠DBC=∠FDE,
∴tan∠DBC=tan∠FDE,
∴![]()
∴![]() =
=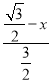 ,
,
解得:x=![]() ,
,
∴tan∠DBC=![]() =
=![]() .
.
故選:D.


科目:初中數學 來源: 題型:
【題目】如圖,經過![]() 和
和![]() 兩點的拋物線
兩點的拋物線![]() 交
交![]() 軸于
軸于![]() 兩點,
兩點,![]() 是拋物線上一動點,平行于
是拋物線上一動點,平行于![]() 軸的直線
軸的直線![]() 經過點
經過點![]() .
.
(1)求拋物線的解析式;
(2)如圖1,![]() 軸上有點
軸上有點![]() 連接
連接![]() ,設點
,設點![]() 到直線
到直線![]() 的距離為
的距離為![]() .
.![]() .小明在探究
.小明在探究![]() 的值的過程中,是這樣思考的:當
的值的過程中,是這樣思考的:當![]() 是拋物線的頂點時,計算
是拋物線的頂點時,計算![]() 的值;當
的值;當![]() 不是拋物線的頂點時,猜想
不是拋物線的頂點時,猜想![]() 是一個定值.請你直接寫出
是一個定值.請你直接寫出![]() 的值,并證明小明的猜想.
的值,并證明小明的猜想.
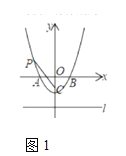
(3)如圖2,點![]() 在第二象限,分別連接
在第二象限,分別連接![]() 、
、![]() ,并延長交直線
,并延長交直線![]() 于
于![]() 兩點.若
兩點.若![]() 兩點的橫坐標分別為
兩點的橫坐標分別為![]() ,試探究
,試探究![]() 之間的數量關系.
之間的數量關系.
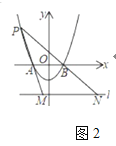
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發現:如圖1,在△ABC中和△DCE中,![]() ,
,![]() ,
,![]() ,點D是BC的垂線AF上任意一點.填空:
,點D是BC的垂線AF上任意一點.填空:
①![]() 的值為 ;
的值為 ;
②∠ABE的度數為 .
(2)類比探究:如圖2,在△ABC中和△DCE中,![]() ,
,![]() ,點D是BC的垂線AF上任意一點.請判斷
,點D是BC的垂線AF上任意一點.請判斷![]() 的值及∠ABE的度數,并說明理由;
的值及∠ABE的度數,并說明理由;
(3) 拓展延伸:在(2)的條件下,若![]() ,
,![]() ,請直接寫出BE的長.
,請直接寫出BE的長.
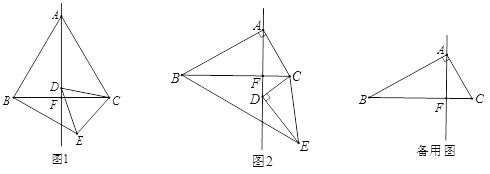
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 位于點
位于點![]() 的左側),與
的左側),與![]() 軸的負半軸交于點
軸的負半軸交于點![]() .
.
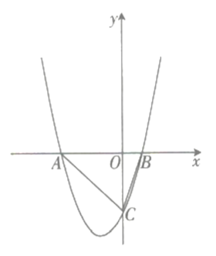
![]() 求點
求點![]() 的坐標.
的坐標.
![]() 若
若![]() 的面積為
的面積為![]() .
.
①求這條拋物線相應的函數解析式.
②在拋物線上是否存在一點![]() 使得
使得![]() ?若存在,請求出點
?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:⊙O的兩條弦![]() ,
,![]() 相交于點
相交于點![]() ,且
,且![]() .
.
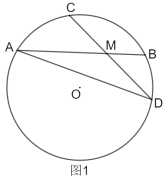
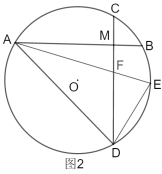
(1)如圖1,連接![]() ,求證:
,求證:![]() .
.
(2)如圖2,在![]() ,在
,在![]() 上取一點
上取一點![]() ,使得
,使得![]() ,
,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.
①判斷![]() 與
與![]() 是否相等,并說明理由.
是否相等,并說明理由.
②若![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在溫度不變的條件下,通過一次又一次地對氣缸頂部的活塞加壓,測出每一次加壓后氣缸內氣體的體積和氣體對汽缸壁所產生的壓強.
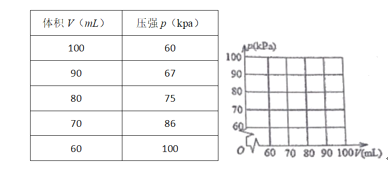
(1)根據表中的數據畫出函數圖像,并求出壓強p(kpa)關于體積V(mL)的函數表達式;
(2)當壓力表讀出的壓強為72kpa時,汽缸內氣體的體積壓縮到多少毫升?
(3)若壓強80<p<90,估計氣缸內氣體體積的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了應對全球新冠肺炎,滿足抗疫物資的需求,某電機公司轉型生產![]() 呼吸機和
呼吸機和![]() 呼吸機,每臺
呼吸機,每臺![]() 呼吸機比每臺
呼吸機比每臺![]() 呼吸機的生產成本多200元,用5萬元生產
呼吸機的生產成本多200元,用5萬元生產![]() 呼吸機與用4.5萬元生產
呼吸機與用4.5萬元生產![]() 呼吸機的數量相等
呼吸機的數量相等
(1)求每臺![]() 呼吸機、
呼吸機、![]() 呼吸機的生產成本各是多少元?
呼吸機的生產成本各是多少元?
(2)該公司計劃生產這兩種呼吸機共50臺進行試銷,其中![]() 呼吸機為
呼吸機為![]() 臺,生產總費用不超過9.8萬元,試銷時
臺,生產總費用不超過9.8萬元,試銷時![]() 呼吸機每臺售價2500元,
呼吸機每臺售價2500元,![]() 呼吸機每臺售價2180元,公司決定從銷售
呼吸機每臺售價2180元,公司決定從銷售![]() 呼吸機的利潤中按每臺捐獻
呼吸機的利潤中按每臺捐獻![]() 元作為公司捐獻國家抗疫的資金,若公司售完50臺呼吸機并捐獻資金后獲得的利潤不超過23000元,求
元作為公司捐獻國家抗疫的資金,若公司售完50臺呼吸機并捐獻資金后獲得的利潤不超過23000元,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市預測某飲料有發展前途,用1600元購進一批飲料,面市后果然供不應求,又用6000元購進這批飲料,第二批飲料的數量是第一批的3倍,但單價比第一批貴2元.
(1)第一批飲料進貨單價多少元?
(2)若二次購進飲料按同一價格銷售,兩批全部售完后,獲利不少于1200元,那么銷售單價至少為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com