
【題目】如圖,四邊形![]() 中,
中, ![]() ,過點
,過點![]() 作
作![]() 的平行線,交
的平行線,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
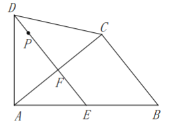
(1)求證:![]() 是
是![]() 的中點.
的中點.
(2)已知![]() ,
,![]() 是射線
是射線![]() 上的動點.設
上的動點.設![]() ,
,
①若四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 關
關![]() 于的函數關系式;
于的函數關系式;
②在①中,當![]() 為何值時,
為何值時,![]() 的周長最小,并求出此時
的周長最小,并求出此時![]() 的值.
的值.
【答案】(1)證明見解析;(2)①![]() ;②
;②![]() ,
,![]() .
.
【解析】
(1)根據平行線的性質求出![]() ,根據
,根據![]() ,推出
,推出![]() ,即可得出答案;
,即可得出答案;
(2)①根據勾股定理求出AC,求出CF的長,得出四邊形BCDP是梯形,根據梯形的面積公式得出即可;
②求出CP+BP最小時,△BCP的周長最小,根據對稱得出當P到E時,△PBC的周長最小,證△DAE∽△ACB,得出比例式,求出DE的值即可.
(1)證明:![]()
![]()
![]()
![]()
![]() ,即
,即![]() 是
是![]() 的中點
的中點
(2)①在Rt△ACB中,AB=15,BC=9,由勾股定理得:
![]()
∵DF∥BC,
∴梯形BCDP的面積y=![]() (x+9)×6=3x+27,
(x+9)×6=3x+27,
即y=3x+27(x>0).
②△PBC的周長是BC+CP+PB=9cm+CP+BP,
要使△PBC的周長最小,只要CP+BP最小即可,
∵CF=AF,DE⊥AC,
∴C、A關于DF對稱,
即當點P運動到點E時,CP+BP最小,此時△PBC的周長最小, 求得AE=BE=![]() AB=
AB=![]() cm,
cm,
∵DE∥BC,
∴∠DEA=∠CBA,
∵∠DAE=∠ACB=90°,
∴△DAE∽△ACB,
∴![]() ,
,
∴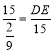 ,
,
![]()
![]() 當
當![]() 時,
時,![]() 的周長最小,此時
的周長最小,此時![]() .
.


科目:初中數學 來源: 題型:
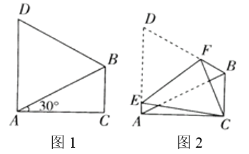
【題目】如圖1,在△ABC中,∠ACB =90°,∠CAB= 30°,△ABD是等邊三角形. 如圖2,將四邊形ACBD折疊,使D與C重合,EF為折痕,則∠ACE的正弦值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前,我國的空氣質量得到了大幅度的提高.現隨機調查了某城市1個月的空氣質量情況,并將監測的結果繪制成如下的兩幅不完整的統計圖.
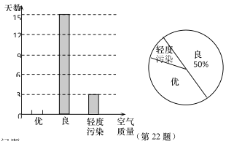
請根據圖中提供的信息,解答下面的問題:
(1)本次調查中,一共調查的天數為_______天;扇形圖中,表示“輕度污染”的扇形的圓心角為______度;
(2)將條形圖補充完整;
(3)估計該城市一年(以365天計算)中,空氣質量未達到優的天數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】扶貧工作小組對果農進行精準扶貧,幫助果農將一種有機生態水果拓寬了市場.與去年相比,今年這種水果的產量增加了1000千克,每千克的平均批發價比去年降低了1元,批發銷售總額比去年增加了![]() .
.
(1)已知去年這種水果批發銷售總額為10萬元,求這種水果今年每千克的平均批發價是多少元?
(2)某水果店從果農處直接批發,專營這種水果.調查發現,若每千克的平均銷售價為41元,則每天可售出300千克;若每千克的平均銷售價每降低3元,每天可多賣出180千克,設水果店一天的利潤為![]() 元,當每千克的平均銷售價為多少元時,該水果店一天的利潤最大,最大利潤是多少?(利潤計算時,其它費用忽略不計.)
元,當每千克的平均銷售價為多少元時,該水果店一天的利潤最大,最大利潤是多少?(利潤計算時,其它費用忽略不計.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是規格為![]() 的正方形網格,請在所給網格中按下列要求操作:
的正方形網格,請在所給網格中按下列要求操作:
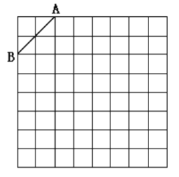
(1)請在網格中建立平面直角坐標系,使點![]() 坐標為
坐標為![]() ,
,![]() 點坐標為
點坐標為![]() ;
;
(2)在第二象限內的格點上畫一點![]() ,使點
,使點![]() 與線段
與線段![]() 組成一個以
組成一個以![]() 為底的等腰三角形,且腰長是無理數, 則
為底的等腰三角形,且腰長是無理數, 則![]() 點坐標是________,
點坐標是________,![]() 的周長是_________(結果保留根號);
的周長是_________(結果保留根號);
(3)畫出![]() 以點
以點![]() 為旋轉中心、旋轉
為旋轉中心、旋轉![]() 后的
后的![]() ,連結
,連結![]() 和
和![]() ,試說出四邊形
,試說出四邊形![]() 是何特殊四邊形, 并說明理由.
是何特殊四邊形, 并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
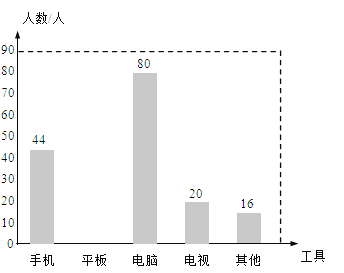
【題目】在“停課不停學”期間,某校數學興趣小組對本校同學觀看教學視頻所使用的工具進行了調查,并從中隨機抽取部分數據進行分析,將分析結果繪制成了兩幅不完整的統計表與統計圖.
工具 | 人數 | 頻率 |
手機 | 44 | a |
平板 | b | 0.2 |
電腦 | 80 | c |
電視 | 20 | d |
不確定 | 16 | 0.08 |
請根據上述信息回答下列問題:
(1)所抽取出來的同學共 人,表中a= ,b= ;
(2)請補全條形統計圖;
(3)若該校觀看教學視頻的學生總人數為2500人,則使用電腦的學生人數約 人.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,平面直角坐標的原點是等邊三角形的中心,A(0,1),把△ABC繞點O順時針旋轉,每秒旋轉60°,則第2017秒時,點A的坐標為( )

A. (0,1) B. (﹣![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學決定在學生中開展丟沙包、打籃球、跳大繩和踢毽球四種項目的活動,為了解學生對四種項目的喜歡情況,隨機調查了該校m名學生最喜歡的一種項目(每名學生必選且只能選擇四種活動項目的一種),并將調查結果繪制成如下的不完整的統計圖表:
學生最喜歡的活動項目的人數統計表
項目 | 學生數(名) | 百分比 |
丟沙包 | 20 | 10% |
打籃球 | 60 | p% |
跳大繩 | n | 40% |
踢毽球 | 40 | 20% |
根據圖表中提供的信息,解答下列問題:
(1)m= ,n= ,p= ;
(2)請根據以上信息直接補全條形統計圖;

(3)根據抽樣調查結果,請你估計該校2000名學生中有多少名學生最喜歡跳大繩.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線L:y=mx2+nx-6經過點(-2,2),與x軸相交于A(-3,0)和B兩點,并與y軸相交于點C.拋物線L′與L關于坐標原點對稱,點A,B在L′上的對應點分別為A′和B′.
(1)求拋物線L的函數表達式.
(2)在拋物線L′上是否存在點P,使得△PA′A的面積等于△CB′B的面積?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com