【題目】（2017浙江省湖州市，第23題，10分）湖州素有魚米之鄉之稱，某水產養殖大戶為了更好地發揮技術優勢，一次性收購了20000kg淡水魚，計劃養殖一段時間后再出售．已知每天放養的費用相同，放養10天的總成本為30.4萬元；放養20天的總成本為30.8萬元（總成本=放養總費用+收購成本）．
（1）設每天的放養費用是a萬元，收購成本為b萬元，求a和b的值；
（2）設這批淡水魚放養t天后的質量為m（kg），銷售單價為y元/kg．根據以往經驗可知：m與t的函數關系為
；y與t的函數關系如圖所示．
①分別求出當0≤t≤50和50＜t≤100時，y與t的函數關系式；
②設將這批淡水魚放養t天后一次性出售所得利潤為W元，求當t為何值時，W最大？并求出最大值．（利潤=銷售總額﹣總成本）
【答案】（1）a的值為0.04，b的值為30；（2）①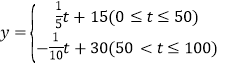
；②放養55天時，W最大，最大值為180250元．
【解析】試題分析：（1）由放養10天的總成本為30.4萬元；放養20天的總成本為30.8萬元可得答案；
（2）①分0≤t≤50、50＜t≤100兩種情況，結合函數圖象利用待定系數法求解可得；
②就以上兩種情況，根據“利潤=銷售總額﹣總成本”列出函數解析式，依據一次函數性質和二次函數性質求得最大值即可得．
試題解析：（1）由題意，得：
，解得：
，答：a的值為0.04，b的值為30；
（2）①當0≤t≤50時，設y與t的函數解析式為y=kt+n，將（0，15）、（50，25）代入，得：
，解得：
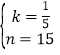，∴y與t的函數解析式為
；
當50＜t≤100時，設y與t的函數解析式為y=at+b，將點（50，25）、（100，20）代入，得：
，解得：
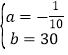，∴y與t的函數解析式為y=﹣
t+30；
綜上所述： ；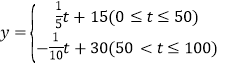
②由題意，當0≤t≤50時，W=20000（
t+15）﹣（400t+300000）=3600t，∵3600＞0，∴當t=50時，W最大值=180000（元）；
當50＜t≤100時，W=（100t+15000）（﹣t+30）﹣（400t+300000）
=﹣10t2+1100t+150000
=﹣10（t﹣55）2+180250，∵﹣10＜0，∴當t=55時，W最大值=180250（元）．
綜上所述，放養55天時，W最大，最大值為180250元．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知Rt△ABC 中，∠ACB=90°，BC=2，AC=3，以點C為圓心、CB為半徑的圓交AB于點D，過點A作AE∥CD，交BC延長線于點E.
（1）求CE的長；
（2）P是 CE延長線上一點，直線AP、CD交于點Q.
①如果△ACQ ∽△CPQ，求CP的長；
②如果以點A為圓心，AQ為半徑的圓與⊙C相切，求CP的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】圖①、圖②、圖③均是4×4的正方形網格，每個小正方形的頂點稱為格點，每個小正方形的邊長均為1.
(1)在圖①、圖②中,以格點為頂點,線段AB為一邊,分別畫一個平行四邊形和菱形,并直接寫出它們的面積.(要求兩個四邊形不全等)
(2)在圖③中，以點A為頂點，另外三個頂點也在格點上，畫一個面積最大的正方形，并直接寫出它的面積。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某餐廳中，一張桌子可坐6人，有如圖所示的兩種擺放方式：
（1）當有n張桌子時，兩種擺放方式各能坐多少人？
（2）一天中午餐廳要接待98位顧客共同就餐，但餐廳只有25張這樣的餐桌.若你是這個餐廳的經理，你打算選擇哪種方式來擺放餐桌？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
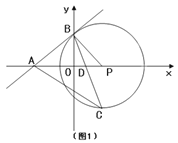
【題目】如圖1，點A、B、P分別在兩坐標軸上，∠APB=60°，PB=m，PA=2m，以點P為圓心、PB為半徑作⊙P，作∠OBP的平分線分別交⊙P、OP于C、D，連接AC．
（1）求證：直線AB是⊙P的切線．
（2）設△ACD的面積為S，求S關于m的函數關系式．
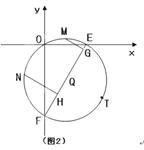
（3）如圖2，當m=2時，把點C向右平移一個單位得到點T，過O、T兩點作⊙Q交x軸、y軸于E、F兩點，若M、N分別為兩弧
的中點，作MG⊥EF，NH⊥EF，垂足為G、H，試求MG+NH的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某中學庫存若干套桌椅，準備修理后支援貧困山區學校。現有甲、乙兩木工組，甲每天修理桌椅16套，乙每天修桌椅比甲多8套，甲單獨修完這些桌椅比乙單獨修完多用20天，學校每天付甲組80元修理費，付乙組120元修理費。
(1)該中學庫存多少套桌椅？
(2)在修理過程中，學校要派一名工人進行質量監督，學校負擔他每天10元生活補助費，現有三種修理方案:a、由甲單獨修理；b、由乙單獨修理；c、甲、乙合作同時修理。你認為哪種方案省時又省錢？為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
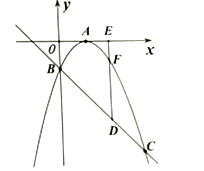
【題目】如圖，已知二次函數
的圖象頂點在
軸上，且
，與一次函數
的圖象交于
軸上一點
和另一交點
.
求拋物線的解析式；
點
為線段
上一點，過點作
軸，垂足為
，交拋物線于點
，請求出線段
的最大值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AD//BC，∠A=∠C，CD=2AD，BE⊥AD于點E，F為CD的中點，連接EF、BF．
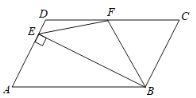
（1）求證：四邊形ABCD是平行四邊形；
（2）求證：BF平分∠ABC；
（3）請判斷△BEF的形狀，并證明你的結論.
查看答案和解析>>
科目：初中數學 來源： 題型：
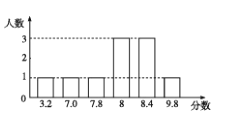
【題目】某學校舉行演講比賽，選出了10名同學擔任評委，并事先擬定從如下4個方案中選擇合理的方案來確定每個演講者的最后得分（滿分為10分）：
方案①：所有評委所給分的平均數；
方案②：在所有評委所給分中，去掉一個最高分和一個最低分，然后再計算其余給分的平均數；
方案③：所有評委所給分的中位數；
方案④：所有評委所給分的眾數。
為了探究上述方案的合理性，先地某個同學的演講成績進行了統計實驗，如圖是這個同學的得分統計圖。
（1）分別按上述4個方案計算這個同學演講的最后得分；
（2）根據（1）中的結果，請用統計的知識說明哪些方案不適合作為這個同學演講的最后得分，并說明你的理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com