
(本小題滿分9分)
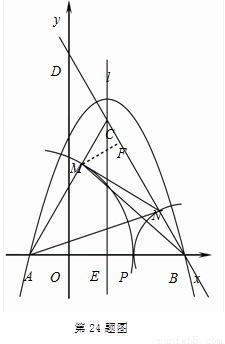
如圖所示,拋物線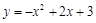 與x軸交于A、B兩點,直線BD的函數表達式為
與x軸交于A、B兩點,直線BD的函數表達式為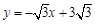 ,拋物線的對稱軸l與直線BD交于點C、與x軸交于點E.
,拋物線的對稱軸l與直線BD交于點C、與x軸交于點E.
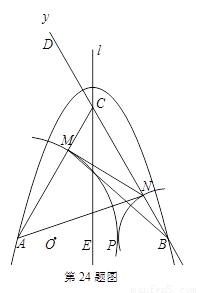
⑴求A、B、C三個點的坐標.
⑵點P為線段AB上的一個動點(與點A、點B不重合),以點A為圓心、以AP為半徑的圓弧與線段AC交于點M,以點B為圓心、以BP為半徑的圓弧與線段BC交于點N,分別連接AN、BM、MN.
①求證:AN=BM.
②在點P運動的過程中,四邊形AMNB的面積有最大值還是有最小值?并求出該最大值或最小值.
(1)A(-1,0),B(3,0) C(1,2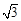 )
)
(2)①AN=BM,證明略。
②m=2時,S取得最小值3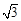
【解析】解:⑴令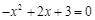 ,
,
解得: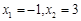 ,
,
∴A(-1,0),B(3,0) 2分
∵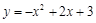 =
=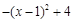 ,
,
∴拋物線的對稱軸為直線x=1,
將x=1代入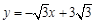 ,得y=2
,得y=2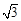 ,
,
∴C(1,2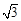 ). 3分
). 3分
⑵①在Rt△ACE中,tan∠CAE= ,
,
∴∠CAE=60º,
由拋物線的對稱性可知l是線段AB的垂直平分線,
∴AC=BC,
∴△ABC為等邊三角形, 4分
∴AB= BC =AC = 4,∠ABC=∠ACB= 60º,
又∵AM=AP,BN=BP,
∴BN = CM,
∴△ABN≌△BCM,
∴AN=BM. 5分
②四邊形AMNB的面積有最小值. 6分
設AP=m,四邊形AMNB的面積為S,
由①可知AB= BC= 4,BN = CM=BP,S△ABC= ×42=
×42= ,
,
∴CM=BN= BP=4-m,CN=m,
過M作MF⊥BC,垂足為F,
則MF=MC•sin60º=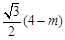 ,
,
∴S△CMN=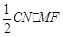 =
=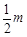 •
•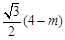 =
=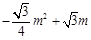 , 7分
, 7分
∴S=S△ABC-S△CMN
= -(
-(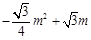 )
)
=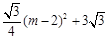 8分
8分
∴m=2時,S取得最小值3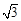 . 9分
. 9分


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
 (本小題滿分6分,請在下列兩個小題中,任選其一完成即可)
(本小題滿分6分,請在下列兩個小題中,任選其一完成即可)查看答案和解析>>
科目:初中數學 來源: 題型:
| 13 |
| 13 |
| 13 |

查看答案和解析>>
科目:初中數學 來源:2011年湖北省荊州市蘆陵中學中考模擬試題(二)數學卷 題型:解答題
(本小題滿分8分)
據2010年5月8日《杭州日報》報道:今年“五一”黃金周期間,我市實現旅游收入再創歷史新高,旅游消費呈現多樣化,各項消費所占的比例如圖秘所示,其中住宿消費為3438.24萬元.
(1)求我市今年“五一”黃金周期間旅游消費共多少億元?旅游消費中各項消費的中位數是多少萬元?
(2)對于“五一”黃金周期間的旅游消費,如果我市2012年要達到3.42億元的目標,那么,2010年到2012年的平均增長率是多少?
2010年杭州市“五一”黃金周旅游各項消費分布統計圖
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com