
【題目】在今年“綠色清明,文明祭祀”活動中,某花店用![]() 元購進若干菊花,很快售完,接著又用
元購進若干菊花,很快售完,接著又用![]() 元購進第二批菊花,已知第二批所購進菊花的數量是第一批所購進菊花數量的
元購進第二批菊花,已知第二批所購進菊花的數量是第一批所購進菊花數量的![]() 倍,且每朵菊花的進價比第一批每朵菊花的進價多
倍,且每朵菊花的進價比第一批每朵菊花的進價多![]() 元.
元.
(1)求第一批每朵瓶菊花的進價是多少元?
(2)若第一批每朵菊花按![]() 元售價銷售,要使總利潤不低于
元售價銷售,要使總利潤不低于![]() 元(不考慮其他因素),第二批每朵菊花的售價至少是多少元?
元(不考慮其他因素),第二批每朵菊花的售價至少是多少元?
【答案】(1)第一批每朵菊花的進價是![]() 元;(2)第二批每朵菊花的售價至少是
元;(2)第二批每朵菊花的售價至少是![]() 元.
元.
【解析】
(1)設第一批每朵菊花的進價是x元,則第一批每朵菊花的進價是(x+1)元,根據數量=總價÷單價結合第二批所購菊花的數量是第一批所購菊花數量的2倍,即可得出關于x的分式方程,解之經檢驗后即可得出結論;
(2)設第二批每朵菊花的售價是y元,根據總利潤=每朵菊花的利潤×銷售數量結合總利潤不低于1500元,即可得出關于y的一元一次不等式,解之取其最小值即可得出結論.
解:(1)設第一批每朵菊花的進價是![]() 元,則第二批每朵菊花的進價是
元,則第二批每朵菊花的進價是![]() 元,
元,
依題意得: ![]()
解得:![]() ,經檢驗,
,經檢驗,![]() 是原方程的解,且符合題意.
是原方程的解,且符合題意.
答:第一批每朵菊花的進價是![]() 元.
元.
(2)設第二批每朵菊花的售價是![]() 元,
元,
依題意,得:![]() ,
,
解得:![]() .
.
答:第二批每朵菊花的售價至少是![]() 元.
元.


科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD與四邊形CEFG是兩個邊長分別為a,b的正方形.
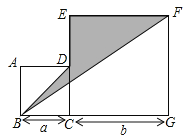
(1)用含a,b的代數式表示三角形BGF的面積;(2)當![]() ,
,![]() 時,求陰影部分的面積.
時,求陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
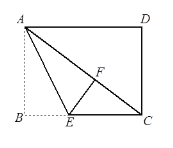
【題目】如圖,已知在長方形ABCD中,將△ABE沿著AE折疊至△AEF的位置,點F在對角線AC上,若BE=3,EC=5,則線段CD的長是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
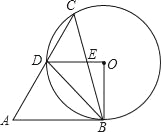
【題目】如圖,在銳角△ABC中,∠A=60°,∠ACB=45°,以BC為弦作⊙O,交AC于點D,OD與BC交于點E,若AB與⊙O相切,則下列結論:
①∠BOD=90°;②DO∥AB;③CD=AD;④△BDE∽△BCD;⑤![]()
正確的有( )
A. ①② B. ①④⑤ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是在汛期中防汛指揮部對某河流做的一星期的水位測量(單位:![]() )
)
(注:此河流的警戒水位為![]() ,“+”表示比河流的警戒水位高,“-”表示比河流的警戒水位低)
,“+”表示比河流的警戒水位高,“-”表示比河流的警戒水位低)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位記錄 | +2.3 | +0.7 | -5.0 | -1.5 | +3.6 | +1.0 | -2.5 |
(1)本周河流水位最高的一天是______,最低的一天是______,這兩天的實際水位分別是_______;
(2)完成下列本周的水位變化表(單位:![]() ),(已知上周末河流的水位比警戒水位低
),(已知上周末河流的水位比警戒水位低![]() .注:規定水位比前一天上升用“+”,比前一天下降用“-”,不升不降用“0”)
.注:規定水位比前一天上升用“+”,比前一天下降用“-”,不升不降用“0”)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位變化 |
(3)與上周末相比,本周末河流水位上升了還是下降了?變化了多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
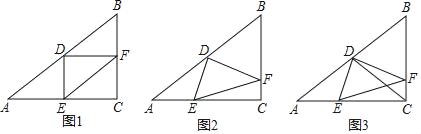
【題目】如圖,已知△ABC中,∠ACB=90°,AC=8,cosA=![]() ,D是AB邊的中點,E是AC邊上一點,聯結DE,過點D作DF⊥DE交BC邊于點F,聯結EF.
,D是AB邊的中點,E是AC邊上一點,聯結DE,過點D作DF⊥DE交BC邊于點F,聯結EF.
(1)如圖1,當DE⊥AC時,求EF的長;
(2)如圖2,當點E在AC邊上移動時,∠DFE的正切值是否會發生變化,如果變化請說出變化情況;如果保持不變,請求出∠DFE的正切值;
(3)如圖3,聯結CD交EF于點Q,當△CQF是等腰三角形時,請直接寫出BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片ABCD中,AB=3,BC=2,沿對角線AC剪開(如圖①);固定△ADC,把△ABC沿AD方向平移(如圖②),當兩個三角形重疊部分的面積最大時,移動的距離AA′等于( )

A. 1 B. 1.5 C. 2 D. 0.8或1.2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料解決問題:兩個多位數整數,若它們各數位上的數字之和相等,則稱這兩個多位數互為“調和數”,例如37和82,它們各數位上的數字之和分別為3+7和8+2,顯然3+7=8+2=10故37和82互為“調和數”.
(1)下列說法錯誤的是
A.123和51互為調和數” ; B.345和513互為“調和數; C.2018和8120互為“調和數”; D.兩位數![]() 和
和![]() 互為“調和數”
互為“調和數”
(2)若A、B是兩個不等的兩位數,A=![]() ,B=
,B=![]() ,A和B互為“調和數”,且A與B之和是B與A之差的3倍,求證:y=-x+9.
,A和B互為“調和數”,且A與B之和是B與A之差的3倍,求證:y=-x+9.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】無錫水蜜桃享譽海內外,老王用3000元購進了一批水蜜桃.第一天,很快以比進價高40% 的價格賣出150千克.第二天,他發現剩余的水蜜桃賣相已不太好,于是果斷地以比進價低20%的價格將剩余的水蜜桃全部售出,本次生意老王一共獲利750元.
(1)根據以上信息,請你編制一個問題,并給予解答;
(2)老王用3000元按第一次的價格又購進了一批水蜜桃.第一天同樣以比進價高40% 的價格賣出150千克,第二天,老王把賣相不好的水蜜桃挑出,單獨打折銷售,售價為10元/千克,結果很快被一搶而空,其余的仍按第一天的價格銷售,且當天全部售完.若老王這次至少獲利1100元,請問打折銷售的水蜜桃最多多少千克?(精確到1千克.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com