【題目】計算：
（1）﹣12+15﹣|﹣7﹣8|
（2）（﹣3）×（﹣9）﹣（﹣5）
（3）
（4）
化簡：（5）
（6）7a+3(a－3b)－2(b－3a)
【答案】（1）﹣12；（2）32；（3）﹣4； （4）
； (5) -3x2+2y-1；(6)16a-11b.
【解析】
（1）先算絕對值里面的，再把絕對值去掉，然后再把所得的數相加即可；
（2）先算乘法，再把減法轉化成加法進行計算即可；
（3）根據乘法的分配律分別進行計算，再把所得的結果相加即可；
（4）根據有理數的混合運算法則分別進行計算，先算乘方，再去括號，然后合并即可；
（5）合并同類項即可；
（6）先去掉括號，再合并同類項即可．
（1）﹣12+15﹣|﹣7﹣8|
=﹣12+15﹣|﹣15|
=﹣12+15﹣15
=﹣12
（2）（﹣3）×（﹣9）﹣（﹣5）
=27+5
=32
（3）
=
=4﹣6﹣2
=﹣4；
（4）
=﹣1﹣
=﹣1﹣
=
；
（5）
=
=-3x2+2y-1
(6)7a+3(a－3b)－2(b－3a)
=7a+3a-9b-2b+6a
=16a-11b
周周清檢測系列答案
輕巧奪冠周測月考直通高考系列答案科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠BAC的角平分線AD交BC于E，交△ABC的外接圓⊙O于D． 
（1）求證：△ABE∽△ADC；
（2）請連接BD，OB，OC，OD，且OD交BC于點F，若點F恰好是OD的中點．求證：四邊形OBDC是菱形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△OAB中，∠OAB=90°，OA=AB=6，將△OAB繞點O逆時針方向旋轉90°
得到△OA1B1 ． 
（1）線段A1B1的長是 ， ∠AOA1的度數是；
（2）連結AA1 ， 求證：四邊形OAA1B1是平行四邊形；
（3）求四邊形OAA1B1的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】當m為何值時，關于x的一元二次方程（2m+1）x2+4mx+2m﹣3=0．
（1）有兩個不相等的實數根；
（2）有兩個相等的實數根；
（3）沒有實數根．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠B=90°，BC=
，∠C=30°．點D從點C出發沿CA方向以每秒2個單位長的速度向點A勻速運動，同時點E從點A出發沿AB方向以每秒1個單位長的速度向點B勻速運動，當其中一個點到達終點時，另一個點也隨之停止運動．設點D、E運動的時間是t秒（t＞0）．過點D作DF⊥BC于點F，連接DE、EF．
（1）求證：AE=DF；
（2）四邊形AEFD能夠成為菱形嗎？如果能，求出相應的t值；如果不能，說明理由．
（3）當t為何值時，△DEF為直角三角形？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明在學習二次根式后，發現一些含根號的式子可以寫成另一個式子的平方，如：3+2
=（1+
）2，善于思考的小明進行了以下探索：
設a+b
=（m+n
）2（其中a、b、m、n均為整數），則有a+b
=m2+2n2+2mn
，∴a=m2+2n2，b=2mn，這樣小明就找到了一種把部分a+b
的式子化為平方式的方法。
請我仿照小明的方法探索并解決下列問題：
（1）當a、b、m、n均為正整數時，若a+b
=（m+n
）2，用含m、n的式子分別表示a、b，得a=________, b=___________.
（2）若a+4
=（m+n
）2，且a、m、n均為正整數，求a的值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在紙面上有一數軸，按要求折疊紙面：
（1）若折疊后數1對應的點與數﹣1對應的點重合，則此時數﹣3對應的點與數 對應的點重合；
（2）若折疊后數2對應的點與數﹣4對應的點重合，則此時數0對應的點與數對 應的點重合；若這樣折疊后，數軸上有A、B兩點也重合，且A、B兩點之間的距離為11（點B在A點的右側），則點A對應的數為 ，點B對應的數為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】百貨商店服裝專柜在銷售中發現：某商品的進價為每件40元．當售價為每件60元時，每星期可賣出300件，現需降價處理，且經市場調查：每降價1元，每星期可多賣出20件．為占有市場份額，在確保盈利的前提下．
（1）降價多少元時，每星期盈利為6125元．
（2）降價多少元時，每星期盈利額最大，最大盈利額是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】未成年人思想道德建設越來越受到社會的關注，遼陽青少年研究所隨機調查了本市一中學100名學生寒假中花零花錢的數量(錢數取整數元)，以便引導學生樹立正確的消費觀．根據調查數據制成了頻
分組 | 頻數 | 頻率 |
0.5～50.5 |
| 0.1 |
50.5～ | 20 | 0.2 |
100.5～150.5 |
|
|
200.5 | 30 | 0.3 |
200.5～250.5 | 10 | 0.1 |
率分布表和頻率分布直方圖(如圖)．
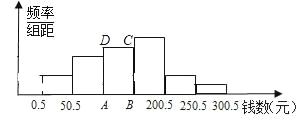
(1)補全頻率分布表；
(2)在頻率分布直方圖中，長方形ABCD的面積是 ；這次調查的樣本容量是 ；
(3)研究所認為，應對消費150元以上的學生提出勤儉節約的建議．試估計應對該校1000名學生中約多少名學生提出這項建議．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com