Question

【題目】如圖甲，直線PA交O于A、E兩點，PA的垂線CD切O于點C，過點A作O的直徑AB.

（1）求證：AC平分∠DAB；
（2）將直線CD向下平行移動，在將直線CD向下平行移動的過程中，如圖乙、丙，試指出與∠DAC相等的角（不要求證明）.
（3）在圖甲中，若DC+DA=6，O的直徑為10，求AE的長度.

Answer 1

【答案】
（1）

證明：如圖1，連接OC，

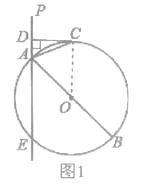
∵OA、OC是O的半徑，

∴ OA=OC.

∴ ∠OAC=∠OCA，

∵CD切于圓O于點C,

∴ CD⊥OC，

又∵CD⊥PA，

∴ OC//PA，

∴ ∠PAC=∠OCA，

∴ ∠OAC=∠PAC，

∴ AC平分∠DAB.

（2）

∠DAC=∠BAF，理由如下：

如圖2，連接BC，

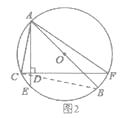
∵AB是圓O的直徑，

∴∠ACB=90°，

∴∠ACF+∠BCF=90°，

又∵在Rt△ACD中，∠DAC+∠ACD=90°，

∴∠DAC=∠FCB，

又∵∠BAF =∠FCB，

∴∠DAC=∠BAF.

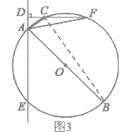
如圖3，∵AB是圓O的直徑，

∴∠ACB=90°，

∴∠CAB+∠CBA=90°，

又∵∠DAF+∠AFD=90°，∠AFD =∠CBA，

∴∠DAF=∠CAB，

∴∠DAF-∠CAF=∠CAB-∠CAF.

∴∠DAC=∠BAF.

（3）

解：如圖4所示：連接OC，過點A作AF⊥CO，垂足為F，連接CB、CE.

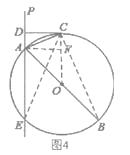
∵DC垂直AE，OC垂直DC，AF垂直CO，

∴ 四邊形AFCD為矩形.

∴ DC=AF，AD=CF.

設AD的長為x，則AF=6-x，OF=5-x.

在Rt△AFO中，OA2=AF2+OF2，即：25=（6-x）2+(5-x)2，

解得：x1=2，x2=9(舍去).

∴ AD=2，DC=4.

由（1）可知：∠DAC=∠BAC，

又∵∠CAD+∠DCA=90°，∠CAB+∠ABC=90°，

∴ ∠DCA=∠ABC，

∵∠DEC=∠ABC，

∴ ∠DEC=∠DCA，

又∵∠EDC=∠ADC，

∴ △EDC~△CDA，

∴ ，即： ，

∴ DE=8,

∴ AE=DE-AD=8-2=6.

【解析】（1）需要證明∠OAC=∠PAC，連接OC，則OC=OA，則∠OAC=∠OCA，所以需要證明∠PAC=∠OCA，則需要證明AD//OC，而CD⊥PA，則CD⊥OC，由CD切于圓O于點C,可證得；（2）如圖2，根據兩角和為90°，等量代換得到∠DAC=∠FCB，由同弧所對的圓周角相等可得∠BAF =∠FCB，從而證得∠DAC=∠BAF；如圖3，同理由兩角和為90°，等量代換得到∠DAF=∠CAB，則∠DAC=∠BAF.（3）連接OC，過點A作AF⊥CO，垂足為F，連接CB、CE，則易得DC=AF，AD=CF，可設AD的長為x，則AF=6-x，OF=5-x，在Rt△AFO中，由勾股定理構造方程解出x，由（1）和（2）可證得∠DEC=∠DCA，又∠EDC=∠ADC，則△EDC~△CDA，由對應邊成比例解出DE，則AE=DE-AD.
【考點精析】認真審題，首先需要了解圓的定義(平面上到定點的距離等于定長的所有點組成的圖形叫做圓．定點稱為圓心，定長稱為半徑)，還要掌握切線的性質定理(切線的性質：1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑)的相關知識才是答題的關鍵．