
【題目】如圖1,已知二次函數![]() (
(![]() 為常數,
為常數,![]() )的圖象過點
)的圖象過點![]() 和點
和點![]() ,函數圖象最低點
,函數圖象最低點![]() 的縱坐標為
的縱坐標為![]() .直線
.直線![]() 的解析式為
的解析式為![]()
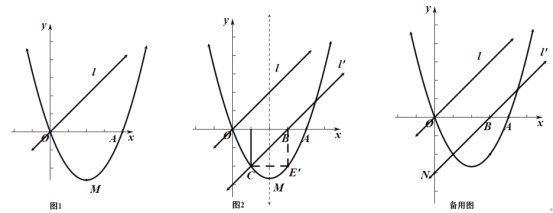
![]() 求二次函數的解析式;
求二次函數的解析式;
![]() 直線
直線![]() 沿
沿![]() 軸向右平移,得直線
軸向右平移,得直線![]() ,
,![]() 與線段
與線段![]() 相交于點
相交于點![]() ,與
,與![]() 軸下方的拋物線相交于點
軸下方的拋物線相交于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,把
,把![]() 沿直線
沿直線![]() 折疊,當點
折疊,當點![]() 恰好落在拋物線上點
恰好落在拋物線上點![]() 時(圖
時(圖![]() 求直線
求直線![]() 的解析式;
的解析式;
![]() 在
在![]() 的條件下,
的條件下,![]() 與
與![]() 軸交于點
軸交于點![]() ,把
,把![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,P為
,P為![]() 上的動點,當
上的動點,當![]() 為等腰三角形時,求符合條件的點
為等腰三角形時,求符合條件的點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)滿足條件的點
;(3)滿足條件的點![]() 坐標為
坐標為![]() 或
或 或
或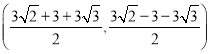
【解析】
(1)先得出拋物線的頂點坐標,從而設出拋物線的頂點式,再將![]() 代入求解即可;
代入求解即可;
(2)設直線![]() 的解析式為
的解析式為![]() ,從而可得點B、
,從而可得點B、![]() 的坐標,再根據翻轉的性質可得四邊形
的坐標,再根據翻轉的性質可得四邊形![]() 是矩形,然后根據對稱性得出點E、C的坐標,最后根據點C、
是矩形,然后根據對稱性得出點E、C的坐標,最后根據點C、![]() 的縱坐標相等列出等式求解即可;
的縱坐標相等列出等式求解即可;
(3)先根據直線![]() 的解析式得出點B、N的坐標,再根據旋轉的性質得出點
的解析式得出點B、N的坐標,再根據旋轉的性質得出點![]() 、
、![]() 的坐標,然后根據等腰三角形的定義,分三種情況,分別根據兩點之間的距離公式求解即可.
的坐標,然后根據等腰三角形的定義,分三種情況,分別根據兩點之間的距離公式求解即可.
(1)由題意得:拋物線的頂點坐標為![]() ,即
,即![]()
由此可設拋物線的解析式為![]()
把![]() 代入得
代入得![]() ,解得
,解得![]()
則拋物線的解析式為![]() ,即
,即![]() ;
;
(2)設直線![]() 沿
沿![]() 軸向右平移m個單位長度,則直線
軸向右平移m個單位長度,則直線![]() 的解析式為
的解析式為![]() ,點B的坐標為
,點B的坐標為![]()
由題意得:![]() ,四邊形
,四邊形![]() 是矩形
是矩形
![]()
![]() 點C與點
點C與點![]() 均在拋物線上
均在拋物線上
![]() 點C與點
點C與點![]() 關于拋物線的對稱軸
關于拋物線的對稱軸![]() 對稱
對稱
![]() 點E與點B關于拋物線的對稱軸
點E與點B關于拋物線的對稱軸![]() 對稱
對稱
![]() 點B的坐標為
點B的坐標為![]()
![]() 點E的坐標為
點E的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]()
![]() 點C的坐標為
點C的坐標為![]()
則![]()
解得![]() 或
或![]() (不符題意,舍去)
(不符題意,舍去)
故直線![]() 的解析式為
的解析式為![]() ;
;
(3)由(2)可知,直線![]() 的解析式為
的解析式為![]() ,點B的坐標為
,點B的坐標為![]()
令![]() 得
得![]() ,則點N的坐標為
,則點N的坐標為![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
把![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]()
則點![]() 在直線
在直線![]() 上,點
上,點![]() 在直線
在直線![]() 上,且
上,且![]() ,
,![]()
![]() 點
點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]()
設![]()
則![]()
![]()
![]()
由等腰三角形的定義,分以下三種情況:
①當![]() 時,即
時,即![]()
則![]()
解得![]()
此時點P的坐標為![]()
②當![]() 時,即
時,即![]()
則![]()
解得![]()
![]()
此時點P的坐標為 或
或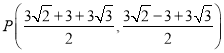
③當![]() 時,即
時,即![]()
則![]()
整理得![]() ,此方程的根的判別式
,此方程的根的判別式![]() ,則此方程沒有實數根
,則此方程沒有實數根
即此時沒有滿足條件的點P
綜上,滿足條件的點![]() 坐標為
坐標為![]() 或
或 或
或
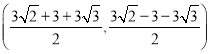 .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系xoy中,二次函數![]() 的圖象與x軸的交點為A,B,頂點為C,點D為點C關于x軸的對稱點,過點A作直線l:
的圖象與x軸的交點為A,B,頂點為C,點D為點C關于x軸的對稱點,過點A作直線l:![]() 交BD于點E,連接BC的直線交直線l于K點.
交BD于點E,連接BC的直線交直線l于K點.
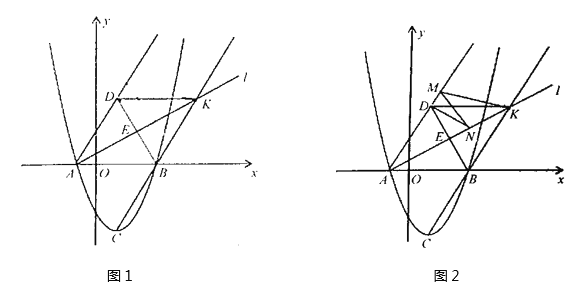
(1)問:在四邊形ABKD內部是否存在點P,使它到四邊形ABKD四邊的距離都相等?
若存在,請求出點P的坐標;若不存在,請說明理由;
(2)若M,N分別為直線AD和直線l上的兩個動點,連結DN,NM,MK,如圖2,求DN+NM+MK和的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2014年鄭州市城鎮民營企業就業人數突破20萬,為了解城鎮民營企業員工每月的收入狀況,統計局對全市城鎮企業民營員工2014年月平均收入隨機抽樣調查,將抽樣的數據按“2000元以內”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分為四組,進行整理,分別用A,B,C,D表示,得到下列兩幅不完整的統計圖.
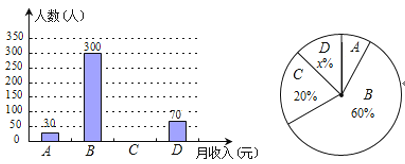
由圖中所給出的信息解答下列問題:
(1)本次抽樣調查的員工有_____人,在扇形統計圖中x的值為_____,表示“月平均收入在2000元以內”的部分所對應扇形的圓心角的度數是_____;
(2)將不完整的條形圖補充完整,并估計我市2013年城鎮民營企業20萬員工中,每月的收入在“2000元~4000元”的約多少人?
(3)統計局根據抽樣數據計算得到,2013年我市城鎮民營企業員工月平均收入為4872元,請你結合上述統計的數據,談一談用平均數反映月收入情況是否合理?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=﹣x2+x+6及一次函數y=﹣x+m,將該二次函數在x軸上方的圖象沿x軸翻折到x軸下方,圖象的其余部分不變,得到一個新函數(如圖所示),請你在圖中畫出這個新圖象,當直線y=﹣x+m與新圖象有4個交點時,m的取值范圍是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中數學 來源: 題型:
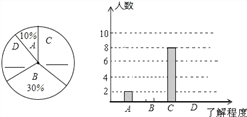
【題目】2013年5月31日是第26個“世界無煙日”,校學生會書記小明同學就“戒煙方式”的了解程度對本校九年級學生進行了一次隨機問卷調查,如圖是他采集數據后繪制的兩幅不完整的統計圖(A:了解較多,B:不了解,C:了解一點,D:非常了解).請你根據圖中提供的信息解答以下問題:
(1)在扇形統計圖中的橫線上填寫缺失的數據,并把條形統計圖補充完整.
(2)2013年該初中九年級共有學生400人,按此調查,可以估計2013年該初中九年級學生中對戒煙方式“了解較多”以上的學生約有多少人?
(3)在問卷調查中,選擇“A”的是1名男生,1名女生,選擇“D”的有4人且有2男2女.校學生會要從選擇“A、D”的問卷中,分別抽一名學生參加活動,請你用列表法或樹狀圖求出恰好是一名男生一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,分別過第二象限內的點![]() 作
作![]() 軸的平行線,與
軸的平行線,與![]() 軸分別交于點
軸分別交于點![]() 與雙曲線
與雙曲線![]() 分別交于點
分別交于點![]()
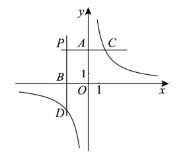
下面四個結論:
①存在無數個點![]() 使
使![]() ;
;
②存在無數個點![]() 使
使![]() ;
;
③至少存在一個點![]() 使
使![]() ;
;
④至少存在一個點![]() 使
使![]() .
.
所有正確結論的序號是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
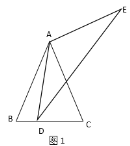
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 邊上一動點,以點
邊上一動點,以點![]() 為頂點,
為頂點,![]() 為一腰作等腰
為一腰作等腰![]() ,使
,使![]() ,且
,且![]() ,設
,設![]() ,
,![]() ,我們稱
,我們稱![]() 為
為![]() 的“頂補三角形”.
的“頂補三角形”.
(1)求![]() 與
與![]() 的數量關系;
的數量關系;
(2)如圖2,![]() 為
為![]() 的“頂補三角形”,過點
的“頂補三角形”,過點![]() 作
作![]() 的平行線,交
的平行線,交![]() 于點
于點![]() ,若四邊形
,若四邊形![]() 是平行四邊形,求證:
是平行四邊形,求證:![]() ;
;
(3)如圖3,四邊形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,
上,![]() ,
,![]() B,
B,![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值.
的值.

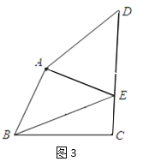
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠ADC=60°,CD=4![]() cm,P為CD的中點.
cm,P為CD的中點.
(1)在AC上找一點Q,使DQ+PQ的值最小(保留畫圖痕跡,不寫畫法,不必說理);
(2)求出(1)中DQ+PQ的長.
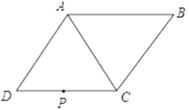
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com