【題目】如圖，在正方形ABCD的外側，作等邊三角形ADE，連接BE，CE．
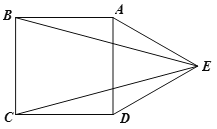
（1）求證：BE=CE．
（2）求∠BEC的度數
【答案】（1）證明見解析；（2）30°
【解析】
試題分析：（1）由正方形和等邊三角形的性質得出AB=AE，DC=DE，∠BAE=150°，∠CDE=150°，可證ΔBAE≌ΔCDE，即可證出BE=CE；
（2）由（1）知：∠AEB=∠CED=15°，從而可求∠BEC的度數．
試題解析：（1）證明：∵四邊形ABCD為正方形
∴AB=AD=CD,∠BAD=∠ ADC=90°
∵三角形ADE為正三角形
∴ AE=AD=DE,∠EAD=∠EDA=60°
∴∠BAE=∠CDE=150°
∴ΔBAE≌ΔCDE
∴BE=CE
（2）∵AB=AD, AD=AE,
∴AB=AE
∴∠ABE=∠AEB
又 ∵∠BAE=150° ∴∠ABE=∠AEB=15°
同理：∠CED=15°
∴∠BEC=600－15°×2=30°
科目：初中數學 來源： 題型：
【題目】為了豐富同學們的課余生活，某學校舉行“親近大自然”戶外活動，現隨機抽取了部分學生進行主題為“你最想去的景點是？”的問卷調查，要求學生只能從“A（植物園），B（花卉園），C（濕地公園），D（森林公園）”四個景點中選擇一項，根據調查結果，繪制了如下兩幅不完整的統計圖．
請解答下列問題：
（1）本次調查的樣本容量是 ；
（2）補全條形統計圖；
（3）若該學校共有3600名學生，試估計該校最想去濕地公園的學生人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P是正方形ABCD的對角線BD上一點(點P不與點B、D重合)，PE⊥BC于點E，PF⊥CD于點F，連接EF給出下列五個結論：①AP＝EF；②AP⊥EF；③僅有當∠DAP＝45°或67.5°時，△APD是等腰三角形；④∠PFE＝∠BAP：⑤
PD＝EC．其中有正確有( )個．
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，正方形
的對角線交于點
點
，
分別在
，
上（
）且
，
，
的延長線交于點
，
，的延長線交于點
，連接
.
（1）求證：
.
（2）若正方形的邊長為4，為
的中點，求的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2019年4月23日是第24個世界讀書日．為了弘揚中華傳統文化，我縣某學校舉辦了“讓讀書成為習慣，讓書香飄滿校園”主題活動，為此特為每個班級訂購了一批新的圖書．初一(1)班訂購老舍文集4套和四大名著2套，總費用為480元；初一(2)班訂購老舍文集2套和四大名著3套，總費用為520元．
(1)求老舍文集和四大名著每套各是多少元？
(2)學校準備再購買老舍文集和四大名著共20套，總費用不超過1720元，購買老舍文集的數量不超過四大名著的3倍，問學校有幾種購買方案，請你設計出來．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
