
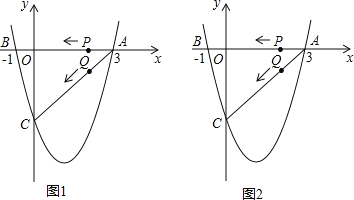
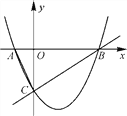
【題目】如圖1(注:與圖2完全相同),二次函數y=![]() x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0)兩點,與y軸交于點C.
x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0)兩點,與y軸交于點C.
(1)求該二次函數的解析式;
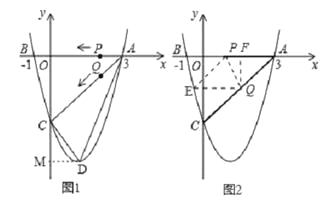
(2)設該拋物線的頂點為D,求△ACD的面積;
(3)若點P,Q同時從A點出發,都以每秒1個單位長度的速度分別沿AB,AC邊運動,其中一點到達端點時,另一點也隨之停止運動,當P,Q運動到t秒時,△APQ沿PQ所在的直線翻折,點A恰好落在拋物線上E點處,請直接判定此時四邊形APEQ的形狀,并求出E點坐標.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)4;(3)四邊形APEQ為菱形,E點坐標為(﹣
x﹣4;(2)4;(3)四邊形APEQ為菱形,E點坐標為(﹣![]() ,﹣
,﹣![]() ).理由詳見解析.
).理由詳見解析.
【解析】試題分析:(1)將A,B點坐標代入函數y=![]() x2+bx+c中,求得b、c,進而可求解析式;(2)由解析式先求得點D、C坐標,再根據S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC,列式計算即可;(3)注意到P,Q運動速度相同,則△APQ運動時都為等腰三角形,又由A、E對稱,則AP=EP,AQ=EQ,易得四邊形四邊都相等,即菱形.利用菱形對邊平行且相等的性質可用t表示E點坐標,又E在E函數上,所以代入即可求t,進而E可表示.
x2+bx+c中,求得b、c,進而可求解析式;(2)由解析式先求得點D、C坐標,再根據S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC,列式計算即可;(3)注意到P,Q運動速度相同,則△APQ運動時都為等腰三角形,又由A、E對稱,則AP=EP,AQ=EQ,易得四邊形四邊都相等,即菱形.利用菱形對邊平行且相等的性質可用t表示E點坐標,又E在E函數上,所以代入即可求t,進而E可表示.
試題解析:(1)∵二次函數y=![]() x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0),
x2+bx+c的圖象與x軸交于A(3,0),B(﹣1,0),
∴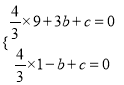 ,
,
解得: 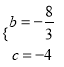 ,
,
∴y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)過點D作DM⊥y軸于點M,
∵y=![]() x2﹣
x2﹣![]() x﹣4=
x﹣4=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,
,
∴點D(1,﹣![]() )、點C(0,﹣4),
)、點C(0,﹣4),
則S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC=![]() ×(1+3)×
×(1+3)×![]() ﹣
﹣![]() ×(
×(![]() ﹣4)×1﹣
﹣4)×1﹣![]() ×3×4=4;
×3×4=4;
(3)四邊形APEQ為菱形,E點坐標為(﹣![]() ,﹣
,﹣![]() ).理由如下
).理由如下
如圖2,E點關于PQ與A點對稱,過點Q作,QF⊥AP于F,
∵AP=AQ=t,AP=EP,AQ=EQ
∴AP=AQ=QE=EP,
∴四邊形AQEP為菱形,
∵FQ∥OC,
∴![]() ,
,
∴![]()
∴AF=![]() t,FQ=
t,FQ=![]() t
t
∴Q(3﹣![]() t,﹣
t,﹣![]() t),
t),
∵EQ=AP=t,
∴E(3﹣![]() t﹣t,﹣
t﹣t,﹣![]() t),
t),
∵E在二次函數y=![]() x2﹣
x2﹣![]() x﹣4上,
x﹣4上,
∴﹣![]() t=
t=![]() (3﹣
(3﹣![]() t)2﹣
t)2﹣![]() (3﹣
(3﹣![]() t)﹣4,
t)﹣4,
∴t=![]() ,或t=0(與A重合,舍去),
,或t=0(與A重合,舍去),
∴E(﹣![]() ,﹣
,﹣![]() ).
).


 高中必刷題系列答案
高中必刷題系列答案科目:初中數學 來源: 題型:
【題目】已知:用2輛A型車和1輛B型車裝滿貨物一次可運貨10噸;用1輛A型車和2輛B型車裝滿貨物一次可運貨11噸,某物流公司現有31噸貨物,計劃同時租用A型車a輛,B型車b輛,一次運轉,且恰好每輛車都裝滿貨物. 根據以上信息,解答下列問題:
(1)1輛A型車和1輛B型車都裝滿貨物一次可分別運貨多少噸?
(2)請你幫該物流公司設計,有幾種租車方案?
(3)若A型車每輛需租金100元/次,B型車每輛需租金120元/次,請選出最省錢的租車方案,并求出最少租車費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了籌備校慶活動,準備印制一批校慶紀念冊.該紀念冊分A、B兩種,每冊都需要10張8K大小的紙,其中A紀念冊有4張彩色頁和6張黑白頁組成;B紀念冊有6張彩色頁和4張黑白頁組成.印制這批紀念冊的總費用由制版費和印制費兩部分組成,制版費與印數無關,價格為:彩色頁300元∕張,黑白頁50元∕張;印制費與總印數的關系見下表.
總印數a(單位:千冊) | 1≤a<5 | 5≤a<10 |
彩色(單位:元∕張) | 2.2 | 2.0 |
黑白(單位:元∕張) | 0.7 | 0.5 |
(1)印制這批紀念冊的制版費為多少元.
(2)若印制A、B兩種紀念冊各2千冊,則共需多少費用?
(3)如果該校共印制了A、B兩種紀念冊6千冊,一共花費了75500元,則該校印制了A、B兩種紀念冊各多少冊?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】個不透明的口袋里裝有分別標有漢字“美”、“麗”、“西”、“湖”的四個小球,除漢字不同之外,小球沒有任何區別,每次摸球前先攪拌均勻再摸球.
(1)若從中任取一個球,球上的漢字剛好是“西”的概率為多少?
(2)甲從中任取一球,不放回,再從中任取一球,請用畫樹狀圖的方法,求出甲取出的兩個球上的漢字恰能組成“美麗”或“西湖”的概率P1;
(3)乙從中任取一球,記下漢字后再放回袋中,再從中任取一球,記乙取出的兩個球上的漢字恰能組成“美麗”或“西湖”的概率為P2,請比較P1,P2的大小關系。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一組數據3,3,2,3,6,3,10,3,6,3,2:①眾數是3;②眾數與中位數的數值不等;③中位數與平均數的數值相等;④平均數與眾數的數值相等,其中正確的結論有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 與x軸交于點B,與y軸交于點C,拋物線
與x軸交于點B,與y軸交于點C,拋物線![]()
與x軸交于A、B兩點(A在B的左側),與y軸交于點C.
(1)求拋物線的解析式;
(2)點M是上述拋物線上一點,如果△ABM和△ABC相似,求點M的坐標;
(3)連接AC,求頂點D、E、F、G在△ABC各邊上的矩形DEFC面積最大時,寫出該矩形在AB邊上的頂點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com