
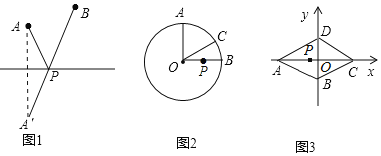
【題目】閱讀材料:“最值問題”是數學中的一類較具挑戰性的問題.其實,數學史上也有不少相關的故事,如下即為其中較為經典的一則:海倫是古希臘精通數學、物理的學者,相傳有位將軍曾向他請教一個問題﹣﹣如圖1,從A點出發,到筆直的河岸l去飲馬,然后再去B地,走什么樣的路線最短呢?海倫輕松地給出了答案:作點A關于直線l的對稱點A′,連接A′B交l于點P,則PA+PB=A′B 的值最小.
解答問題:
(1)如圖2,⊙O的半徑為2,點A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一動點,求PA+PC的最小值;
(2)如圖3,已知菱形ABCD的邊長為6,∠DAB=60°.將此菱形放置于平面直角坐標系中,各頂點恰好在坐標軸上.現有一動點P從點A出發,以每秒2個單位的速度,沿A→C的方向,向點C運動.當到達點C后,立即以相同的速度返回,返回途中,當運動到x軸上某一點M時,立即以每秒1個單位的速度,沿M→B的方向,向點B運動.當到達點B時,整個運動停止.
①為使點P能在最短的時間內到達點B處,則點M的位置應如何確定?
②在①的條件下,設點P的運動時間為t(s),△PAB的面積為S,在整個運動過程中,試求S與t之間的函數關系式,并指出自變量t的取值范圍.
【答案】(1)PA+PC的最小值是2![]() ;(2)①點M的位置是(
;(2)①點M的位置是(![]() ,0)時,用時最少;②S與t之間的函數關系式是當3
,0)時,用時最少;②S與t之間的函數關系式是當3![]() <t≤4
<t≤4![]() 時,S=18
時,S=18![]() ﹣3t;當0<t≤3
﹣3t;當0<t≤3![]() 時,S=3t.當4
時,S=3t.當4![]() <t≤6
<t≤6![]() 時,S=﹣3t+18
時,S=﹣3t+18![]() .
.
【解析】
(1)延長AO交圓O于M,連接CM交OB于P,連接AC,AP+PC=PC+PM=CM最小;
(2)①根據運動速度不同以及運動距離,得出當PB⊥AB時,點P能在最短的時間內到達點B處;
②根據三角形的面積公式求出從A到C時,s與t的關系式和從C到(![]() ,0)以及到B的解析式.
,0)以及到B的解析式.
解:(1)延長AO交圓O于M,連接CM交OB于P,連接AC,
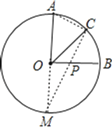
則此時AP+PC=PC+PM=CM最小,
∵AM是直徑,∠AOC=60°,
∴∠ACM=90°,∠AMC=30°,
∴AC=![]() AM=2,AM=4,由勾股定理得:CM=
AM=2,AM=4,由勾股定理得:CM=![]() =2
=2![]() .
.
答:PA+PC的最小值是2![]() .
.
(2)①根據動點P從點A出發,以每秒2個單位的速度,沿A→C的方向,向點C運動.當到達點C后,立即以相同的速度返回,返回途中,當運動到x軸上某一點M時,立即以每秒1個單位的速度,沿M→B的方向,向點B運動,即為使點P能在最短的時間內到達點B處,
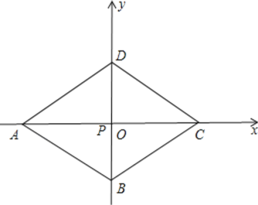
∴當PB⊥AB時,根據垂線段最短得出此時符合題意,
∵菱形ABCD,AB=6,∠DAB=60°,
∴∠BAO=30°,AB=AD,AC⊥BD,
∴△ABD是等邊三角形,
∴BD=6,BO=3,由勾股定理得:AO=3![]() ,
,
在Rt△APB中,AB=6,∠BAP=30°,BP=![]() AP,由勾股定理得:AP=4
AP,由勾股定理得:AP=4![]() ,BP=2
,BP=2![]() ,
,
∴點M的位置是(![]() ,0)時,用時最少.
,0)時,用時最少.
②當0<t≤3![]() 時,AP=2t,
時,AP=2t,
∵菱形ABCD,
∴∠OAB=30°,
∴OB=![]() AB=3,
AB=3,
由勾股定理得:AO=CO=3![]() ,
,
∴S=![]() AP×BO=
AP×BO=![]() ×2t×3=3t;
×2t×3=3t;
③當3![]() <t≤4
<t≤4![]() 時,AP=6
時,AP=6![]() ﹣(2t﹣6
﹣(2t﹣6![]() )=12
)=12![]() ﹣2t,
﹣2t,
∴S=![]() AP×BO=
AP×BO=![]() ×(12
×(12![]() ﹣2t)×3=18
﹣2t)×3=18![]() ﹣3t.
﹣3t.
當4![]() <t≤6
<t≤6![]() 時,
時,
S=![]() AB×BP=
AB×BP=![]() ×6×[2
×6×[2![]() ﹣(t﹣4
﹣(t﹣4![]() )]=﹣3t+18
)]=﹣3t+18![]() ,
,
答:S與t之間的函數關系式是當3![]() <t≤4
<t≤4![]() 時,S=18
時,S=18![]() ﹣3t;當0<t≤3
﹣3t;當0<t≤3![]() 時,S=3t.當4
時,S=3t.當4![]() <t≤6
<t≤6![]() 時,S=﹣3t+18
時,S=﹣3t+18![]() .
.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源: 題型:
【題目】科幻小說《流浪地球》的銷量急劇上升.為應對這種變化,某網店分別花20000元和30000元先后兩次購進該小說,第二次的數量比第一次多500套,且兩次進價相同.
(1)該科幻小說第一次購進多少套?每套進價多少元?
(2)根據以往經驗:當銷售單價是25元時,每天的銷售量是250套;銷售單價每上漲1元,每天的銷售量就減少10套.網店要求每套書的利潤不低于10元且不高于18元.
①直接寫出網店銷售該科幻小說每天的銷售量y(套)與銷售單價x(元)之間的函數關系式及自變量x的取值范圍;
②網店店主期盼最高日利潤達到2500元,他的愿望能實現嗎?請你說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
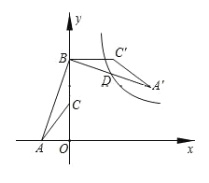
【題目】如圖,點A的坐標是(-2,0),點B的坐標是(0,6),C為OB的中點,將△ABC繞點B逆時針旋轉90°后得到△A′BC′,若反比例函數![]() 的圖像恰好經過A′B的中點D,求這個反比例函數的解析式.
的圖像恰好經過A′B的中點D,求這個反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班同學積極響應“陽光體育工程”的號召,利用課外活動時間積極參加體育鍛煉,每位同學從長跑、籃球、鉛球、立定跳遠中選一項進行訓練,訓練前后郗進行了測試.現將項目選擇情況及訓練前后籃球定時定點投測試成績整理作出如下統計圖表.
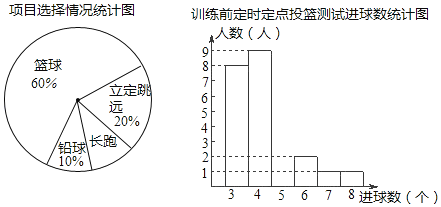
訓練后籃球定時定點投籃測試進球數統計表:
進球數(個) | 8 | 7 | 6 | 5 | 4 | 3 |
人數 | 2 | 1 | 4 | 7 | 8 | 2 |
請你根據圖表中的信息回答下列問題
(1)送擇長跑訓練的人數占全班人數的百分比是 ,該班共有同學 人;
(2)直接補全“訓練前籃球定時定點投測試進球數統計圖”;
(3)若全區共有該年級學生4000人,請估計參加訓練后籃球定時定點投籃進球數達到6個以上(包含6個)多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養雞場有2500只雞準備對外出售.從中隨機抽取了一部分雞,根據它們的質量(單位:![]() ),繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:
),繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:

(Ⅰ)圖①中![]() 的值為 ;
的值為 ;
(Ⅱ)求統計的這組數據的平均數、眾數和中位數;
(Ⅲ) 根據樣本數據,估計這2500只雞中,質量為![]() 的約有多少只?
的約有多少只?
查看答案和解析>>
科目:初中數學 來源: 題型:
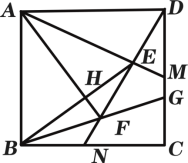
【題目】如圖,在正方形ABCD中,AB=2,M為CD的中點,N為BC的中點,連接AM和DN交于點E,連接BE,作AH⊥BE于點H,延長AH與DN交于點F.連接BF并延長與CD交于點G,則MG的長度為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正方形ABCD與等腰直角三角形EFG如圖擺放,若點M、N剛好是AD的三等分點,下列結論正確的是( )
①△AMH≌△NME;②![]() ;③GH⊥EF;④S△EMN:S△EFG=1:16
;③GH⊥EF;④S△EMN:S△EFG=1:16
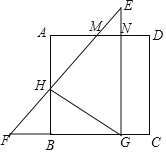
A.①②③④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
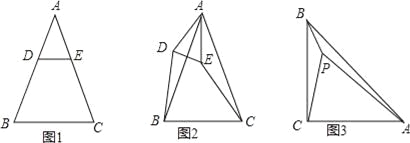
【題目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如圖1,當DE∥BC時,有DB EC.(填“>”,“<”或“=”)
(2)發現探究:若將圖1中的△ADE繞點A順時針旋轉α(0°<α<180°)到圖2位置,則(1)中的結論還成立嗎?若成立,請給予證明;若不成立,請說明理由.
(3)拓展運用:如圖3,P是等腰直角三角形ABC內一點,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com