
【題目】如圖,矩形ABCD的頂點 A的坐標為(4,2),頂點B,C分別在![]() 軸,
軸,![]() 軸的正半軸上.
軸的正半軸上.
(1)求證:∠OCB=∠ABE;
(2)求OC長的取值范圍;
(3)若D的坐標為(![]() ,
,![]() ),請說明
),請說明![]() 隨
隨![]() 的變化情況.
的變化情況.

【答案】(1)證明見解析;(2)0<OC≤2.(3)當0<![]() ≤2時,
≤2時,![]() 隨
隨![]() 的增大而增大;當2≤
的增大而增大;當2≤![]() <2時,
<2時,![]() 隨
隨![]() 的增大而減小.
的增大而減小.
【解析】試題分析:(1)根據矩形的性質得出∠CBA=∠COB=90°,求出∠OCB+∠CBO=90°,∠CBO+∠ABE=90°,即可得出答案;(2)過A作AF⊥x軸于F,證△COB∽△BEA,得出比例式,設OB=x,OC=y,則BE=4﹣x,求出y=﹣x2+2x=﹣![]() (x﹣2)2+2,即可得出答案;(3)求出n=﹣
(x﹣2)2+2,即可得出答案;(3)求出n=﹣![]() (m﹣2)2+4,根據二次函數的性質得出即可.
(m﹣2)2+4,根據二次函數的性質得出即可.
試題解析:
(1)證明:∵矩形ABCD,
∴∠ABC=90°,
∵∠BOC=90°,
∴∠ABC=∠BOC,
∵∠BOC+∠OCB=∠ABC+∠ABE,
∴∠OCB=∠ABE.
(2)解:過點A作AF⊥![]() 軸于F,
軸于F,
當點B在點F時,OC的長最小,為0.
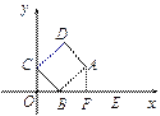
設OB=![]() ,OC=
,OC=![]() ,則BF=4-
,則BF=4-![]() .
.
∵AF⊥![]() 軸,
軸,
∴∠AFB=90°.
∴∠BOC=∠AFB=90°.
∴△BOC∽△AEB.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴OC的最大值為2.
∴OC的取值范圍是0<OC≤2.
(3)解:過點D作AH⊥![]() 軸于H.
軸于H.
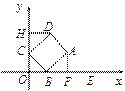
由矩形的性質易得△DHC≌△BFA.
∴DH=BF=4-![]() ,
,
CH=AF=2.
∴![]() ,
,![]() .
.
∴![]() .
.
∵0≤![]() <4,
<4,
∴0<![]() ≤4.
≤4.
∴當0<![]() ≤2時,
≤2時,![]() 隨
隨![]() 的增大而增大;當2≤
的增大而增大;當2≤![]() <2時,
<2時,![]() 隨
隨![]() 的增大而減小.
的增大而減小.


科目:初中數學 來源: 題型:
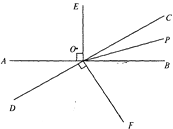
【題目】.如圖,直線AB與CD相交于點O,OP是∠BOC的平分線,OE⊥AB,OF⊥CD,
(1)圖中除直角外,還有相等的角嗎?請寫出兩對:①____________;②____________.
(2)如果∠AOD=40°,則①∠BOC=_______;②OP是∠BOC的平分線,所以∠COP=______度;
③求∠BOF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公園門票的收費標準如下:
門票類別 | 成人票 | 兒童票 | 團體票(限5張及以上) |
價格(元/人) | 100 | 40 | 60 |
有兩個家庭分別去該公園游玩,每個家庭都有5名成員,且他們都選擇了最省錢的方案購買門票,結果一家比另一家少花40元,則花費較少的一家花了_____元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】線段CD是由線段AB平移得到的,點A(﹣1,4)的對應點為C(4,7),則點D(1,2)的對應點B的坐標為( )
A.(2,9)B.(5,3)C.(﹣4,﹣1)D.(﹣9,﹣4)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,平行四邊形ABCD的頂點A(0,2)、B(1,0)在x軸、y軸上,另兩個頂點C、D在第一象限內,且AD=3AB.若反比例函數y=kx-1(k>0)的圖象經過C,D兩點,則k的值是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】哈爾濱市10月份平均氣溫為4℃,11月份平均氣溫為﹣10℃,則11月份的平均氣溫比10月份的平均氣溫低( )℃.
A.﹣14B.14C.﹣6D.6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com