
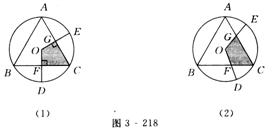
如圖3-218(1)所示,圓內接△ABC中,AB=BC=CA,OD,OE為⊙O的半徑,OD⊥BC于點F,OE⊥AC于點G.
(1)求證陰影部分四邊形OFCG的面積是△ABC面積的 ;
;
(2)如圖3-218(2)所示,若∠DOE保持120°角度不變,求證當∠DOE繞著O點旋轉時,由兩條半徑和△ABC的兩條邊圍成的圖形(圖中陰影部分)面積始終是△ABC的面積的 .
.
(1)證明:連接OA,OC,∵點O是等邊三角形ABC的外心,Rt△OFC≌Rt△OGC≌Rt△OGA,S四邊形OFCG=2S△OFC=S△OAC.∵S△OAC= S△ABC,∴S四邊形OFCG=
S△ABC,∴S四邊形OFCG= S
S △
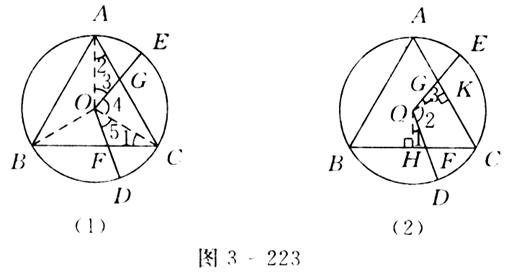
△ ABC. (2)證法1:如圖3-223(1)所示,連接OA,OB和OC,則△AOC≌△COB≌△BOA,∠1=∠2.不妨設OD交BC于點F,OE交AC于點G,∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,∴∠3=∠5.在△OAG和△OCF中,
ABC. (2)證法1:如圖3-223(1)所示,連接OA,OB和OC,則△AOC≌△COB≌△BOA,∠1=∠2.不妨設OD交BC于點F,OE交AC于點G,∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,∴∠3=∠5.在△OAG和△OCF中,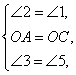 ∴△OAG≌△OCF,∴S四邊形OFCG=S△AOC=
∴△OAG≌△OCF,∴S四邊形OFCG=S△AOC= S△ABC.證法2:如圖3-223(2)所示,不妨設OD交BC于點F,OE交AC于點G,作DH⊥BC,OK⊥AC,垂足分別為點H,K.在四邊形HOKC中,∠OHC=∠OKC=90°,∠C=60°,∴∠HOK=360
S△ABC.證法2:如圖3-223(2)所示,不妨設OD交BC于點F,OE交AC于點G,作DH⊥BC,OK⊥AC,垂足分別為點H,K.在四邊形HOKC中,∠OHC=∠OKC=90°,∠C=60°,∴∠HOK=360 °-90°-90°-60°=120°,即∠1+∠2=120°.又∵∠GOF=∠2+∠3=120°∴∠1=∠3.∵AC=BC,∴OH=OK.又∠OHF=∠OKG=90°.∴△OFH≌△OGK,∴S四邊形OFCG=S四邊形OHCK=
°-90°-90°-60°=120°,即∠1+∠2=120°.又∵∠GOF=∠2+∠3=120°∴∠1=∠3.∵AC=BC,∴OH=OK.又∠OHF=∠OKG=90°.∴△OFH≌△OGK,∴S四邊形OFCG=S四邊形OHCK= S△ABC.
S△ABC.


科目:初中數學 來源: 題型:
.在平面直角坐標系內,點O為坐標原點,二次函數y=x2+(k-5)x-(k+4)的圖象交x軸于點A(x1,0),B(x2,0),且(xl+1)(x2+1)=-8.
(1)求二次函數的解析式;
(2)將上述二次函數圖象沿x軸向右平移2個單位長度,設平移后的圖象交y軸于點C,頂點為P,求△POC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖l—1 27所示,在平面直角坐標系中,將矩形OABC沿OB對折,使點A落在A1處,已知AO=
27所示,在平面直角坐標系中,將矩形OABC沿OB對折,使點A落在A1處,已知AO=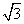 ,AB=1,則點A1的坐標是 ( )
,AB=1,則點A1的坐標是 ( )
A.(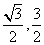 ) B.(
) B.(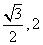 ) C.(
) C.(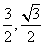 ) D.(
) D.(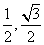 )
)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com