
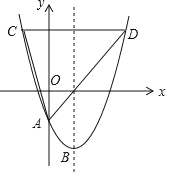
【題目】如圖,在平面直角坐標(biāo)系中,拋物線y=a(x﹣2)2﹣4與y軸交于點(diǎn)A,頂點(diǎn)為B,點(diǎn)A的坐標(biāo)為(0,﹣2),點(diǎn)C在拋物線上(不與點(diǎn)A,B重合),過(guò)點(diǎn)C作y軸的垂線交拋物線于點(diǎn)D,連結(jié)AC,AD,CD,設(shè)點(diǎn)C的橫坐標(biāo)為m.
(1)求這條拋物線所對(duì)應(yīng)的函數(shù)表達(dá)式.
(2)用含m的代數(shù)式表示線段CD的長(zhǎng).
(3)點(diǎn)E是拋物線對(duì)稱軸上一點(diǎn),且點(diǎn)E的縱坐標(biāo)比點(diǎn)C的縱坐標(biāo)小1,連結(jié)BD,DE,設(shè)△ACD的面積為S1,△BDE的面積為S2,且S1S2≠0,求S2=![]() S1時(shí)m的值.
S1時(shí)m的值.
(4)將拋物線y=a(x﹣2)2﹣4沿x=2平移,得到拋物線y=a(x﹣2)2+k,過(guò)點(diǎn)C作y軸平行線與拋物線y=a(x﹣2)2+k交于點(diǎn)F,若CD與y軸交于點(diǎn)G,且CD=6,直接寫出使AC=FG的點(diǎn)F的坐標(biāo).
【答案】(1)y=![]() x2﹣2x﹣2;(2)當(dāng)m<2,且m≠0時(shí),CD=4﹣2m;當(dāng)m>2時(shí),CD=2m﹣4;(3)m=2±
x2﹣2x﹣2;(2)當(dāng)m<2,且m≠0時(shí),CD=4﹣2m;當(dāng)m>2時(shí),CD=2m﹣4;(3)m=2±![]() 或m=
或m=![]() ;(4)點(diǎn)F的坐標(biāo)為(﹣1,﹣2)或(﹣1,3)或(5,﹣2)或(5,3)
;(4)點(diǎn)F的坐標(biāo)為(﹣1,﹣2)或(﹣1,3)或(5,﹣2)或(5,3)
【解析】試題分析:(1)把A(0,-2)代入拋物線切線a=![]() 即可;
即可;
(2)拋物線的對(duì)稱軸為直線x=2,且點(diǎn)C的橫坐標(biāo)為m,得出當(dāng)m<2,且m≠0時(shí),CD=4-2m,當(dāng)m>2時(shí),CD=2m-4;
(3)求出BE=![]() m2-2m+1或BE=-
m2-2m+1或BE=-![]() m2+2m-1,由三角形面積關(guān)系得出方程,解方程即可;
m2+2m-1,由三角形面積關(guān)系得出方程,解方程即可;
(4)由題意得出則四邊形AGCF是矩形,求出點(diǎn)C的坐標(biāo),分情況討論,根據(jù)點(diǎn)的坐標(biāo)關(guān)系即可得出答案.
試題解析:(1)∵拋物線y=a(x﹣2)2﹣4與y軸交于點(diǎn)A(0,﹣2),
∴﹣2=4a﹣4,
解得:a=![]() ,
,
∴這條拋物線所對(duì)應(yīng)的函數(shù)表達(dá)式為y=![]() (x﹣2)2﹣4,
(x﹣2)2﹣4,
即y=![]() x2﹣2x﹣2;
x2﹣2x﹣2;
(2)∵拋物線y=![]() (x﹣2)2﹣4的對(duì)稱軸為直線x=2,且點(diǎn)C的橫坐標(biāo)為m,
(x﹣2)2﹣4的對(duì)稱軸為直線x=2,且點(diǎn)C的橫坐標(biāo)為m,
∴當(dāng)m<2,且m≠0時(shí),CD=4﹣2m;
當(dāng)m>2時(shí),CD=2m﹣4;
(3)∵B(2,﹣4),E(2, ![]() m2﹣2m﹣3),
m2﹣2m﹣3),
∴BE=![]() m2﹣2m+1或BE=﹣
m2﹣2m+1或BE=﹣![]() m2+2m﹣1,
m2+2m﹣1,
∴S1=![]() CD(
CD(![]() m2﹣2m)或S1=
m2﹣2m)或S1=![]() CD(﹣
CD(﹣![]()
![]() CD(
CD(![]() m2﹣2m+1)或S2=
m2﹣2m+1)或S2=![]() CD(﹣
CD(﹣![]() m2+2m﹣1),
m2+2m﹣1),
∵S2=![]() S1,
S1,
∴4(![]() m2﹣2m)=3(
m2﹣2m)=3(![]() m2﹣2m+1),或4(
m2﹣2m+1),或4(![]() m2﹣2m)=﹣3(
m2﹣2m)=﹣3(![]() m2﹣2m+1),
m2﹣2m+1),
解得:m=2±![]() 或=
或=![]() ;
;
(4)若AC=FG,連接AF,則四邊形AGCF是矩形,
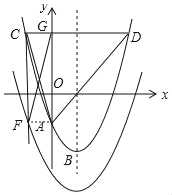
∵CD=6,拋物線的對(duì)稱軸為x=2,
∴點(diǎn)C的橫坐標(biāo)為﹣1或5;
①當(dāng)點(diǎn)C的橫坐標(biāo)為﹣1時(shí),點(diǎn)C的縱坐標(biāo)=![]() ×(﹣1)2﹣2×(﹣1)﹣2=
×(﹣1)2﹣2×(﹣1)﹣2=![]() ,
,
當(dāng)拋物線向下平移時(shí),如圖所示,
∵點(diǎn)A的坐標(biāo)為(0,﹣2),
∴點(diǎn)F的坐標(biāo)為(﹣1,﹣2);
當(dāng)拋物線向上平移時(shí),同理得出點(diǎn)F的坐標(biāo)為(﹣1,3);
②當(dāng)點(diǎn)C的橫坐標(biāo)為5時(shí),點(diǎn)C的縱坐標(biāo)為![]() ,
,
當(dāng)拋物線向下平移時(shí),同理的點(diǎn)F的坐標(biāo)為(5,﹣2);
當(dāng)拋物線向上平移時(shí),同理得出點(diǎn)F的坐標(biāo)為(5,3);
綜上所述:點(diǎn)F的坐標(biāo)為(﹣1,﹣2)或(﹣1,3)或(5,﹣2)或(5,3).


 應(yīng)用題天天練四川大學(xué)出版社系列答案
應(yīng)用題天天練四川大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在第1個(gè)![]() 中,
中,![]() 40°,
40°,![]() ,在
,在![]() 上取一點(diǎn)
上取一點(diǎn)![]() ,延長(zhǎng)
,延長(zhǎng)![]() 到
到![]() ,使得在第2個(gè)
,使得在第2個(gè)![]() 中,
中,![]() ;在
;在![]() 上取一點(diǎn)
上取一點(diǎn)![]() ,延長(zhǎng)
,延長(zhǎng)![]() 到
到![]() ,使得在第3個(gè)
,使得在第3個(gè)![]() 中,
中,![]() ;…,按此做法進(jìn)行下去,第3個(gè)三角形中以
;…,按此做法進(jìn)行下去,第3個(gè)三角形中以![]() 為頂點(diǎn)的內(nèi)角的度數(shù)為_____; 第
為頂點(diǎn)的內(nèi)角的度數(shù)為_____; 第![]() 個(gè)三角形中以
個(gè)三角形中以![]() 為頂點(diǎn)的內(nèi)角的度數(shù)為_____度.
為頂點(diǎn)的內(nèi)角的度數(shù)為_____度.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在□ABCD 中,以點(diǎn) A 為圓心,AB 長(zhǎng)為半徑畫弧交 AD 于點(diǎn) F,再分別以點(diǎn) B、F 為圓心,大于![]() BF 的相同長(zhǎng)為半徑畫弧,兩弧交于點(diǎn) P,連接 AP 并延長(zhǎng)交 BC 于點(diǎn) E,連接 EF.
BF 的相同長(zhǎng)為半徑畫弧,兩弧交于點(diǎn) P,連接 AP 并延長(zhǎng)交 BC 于點(diǎn) E,連接 EF.
(1)根據(jù)以上尺規(guī)作圖的過(guò)程,證明四邊形 ABEF 是菱形;
(2)若菱形 ABEF 的邊長(zhǎng)為 2,AE= 2 ![]() ,求菱形 ABEF 的面積.
,求菱形 ABEF 的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】出租車司機(jī)張師傅某天上午營(yíng)運(yùn)全是在東西向的長(zhǎng)江路上進(jìn)行的,如果向東為正,向西為負(fù),這天上午他行車?yán)锍蹋▎挝唬?/span>km)如下:
![]() .
.
⑴.最后一名乘客送到目的地,出租車在東面還是西面?在多少千米處?
⑵.請(qǐng)你幫張師傅算一下,這天上午他一共行駛了多少里程?
⑶.若每千米耗油0.1L,則這天上午張師傅一共用了多少升油?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在等腰直角![]() 中,
中,![]() ,D是線段
,D是線段![]() 上一點(diǎn)(
上一點(diǎn)(![]() ),連接
),連接![]() ,過(guò)點(diǎn)C作
,過(guò)點(diǎn)C作![]() 的垂線,交
的垂線,交![]() 的延長(zhǎng)線于點(diǎn)E,交
的延長(zhǎng)線于點(diǎn)E,交![]() 的延長(zhǎng)線于點(diǎn)F.
的延長(zhǎng)線于點(diǎn)F.
(1)依題意補(bǔ)全圖形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)若點(diǎn)G在線段![]() 上,
上,![]() ,連接
,連接![]() .
.
①判斷![]() 與
與![]() 的位置關(guān)系并證明;
的位置關(guān)系并證明;
②用等式表示![]() 之間的數(shù)量關(guān)系.
之間的數(shù)量關(guān)系.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
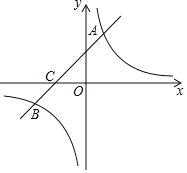
【題目】如圖,在平面直角坐標(biāo)系中,一次函數(shù)![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() 的圖象相交于第一、三象限內(nèi)的
的圖象相交于第一、三象限內(nèi)的![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
⑴求該反比例函數(shù)和一次函數(shù)的解析式;
⑵在![]() 軸上找一點(diǎn)
軸上找一點(diǎn)![]() 使
使![]() 最大,求
最大,求![]() 的最大值及點(diǎn)
的最大值及點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
⑶直接寫出當(dāng)![]() 時(shí),
時(shí),![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】解:根據(jù)算術(shù)平方根的意義,由![]() ,得(2x-y)2=9,所以2x-y=3.①(第一步)
,得(2x-y)2=9,所以2x-y=3.①(第一步)
根據(jù)立方根的意義,由![]() ,得x-2y=-3.②(第二步)
,得x-2y=-3.②(第二步)
解得x=3,y=3.
把x、y的值代入分式中,得![]() .(第三步)
.(第三步)
上述解答有兩處錯(cuò)誤,一處是___________步,忽視了___________;另一處是步___________,忽視了___________.請(qǐng)寫出正確的解答過(guò)程.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】求出下列x的值:
(1)4x2﹣81=0; (2)64(x+1)3=27;
(3)-(x-3)3=27 (4)9(3x+2)2-64=0;
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com