
已知:如圖,直線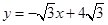 與x軸相交于點(diǎn)A,與直線
與x軸相交于點(diǎn)A,與直線 相交于點(diǎn)P.動(dòng)點(diǎn)E從原點(diǎn)O出發(fā),以每秒1個(gè)單位長(zhǎng)度的速度沿著OPA的路線向點(diǎn)A勻速運(yùn)動(dòng)(E不與點(diǎn)O,A重合),過(guò)點(diǎn)E分別作EF⊥x軸于F,EB⊥y軸于B.設(shè)運(yùn)動(dòng)t秒時(shí),矩形EBOF與△OPA重疊部分面積為S.
相交于點(diǎn)P.動(dòng)點(diǎn)E從原點(diǎn)O出發(fā),以每秒1個(gè)單位長(zhǎng)度的速度沿著OPA的路線向點(diǎn)A勻速運(yùn)動(dòng)(E不與點(diǎn)O,A重合),過(guò)點(diǎn)E分別作EF⊥x軸于F,EB⊥y軸于B.設(shè)運(yùn)動(dòng)t秒時(shí),矩形EBOF與△OPA重疊部分面積為S.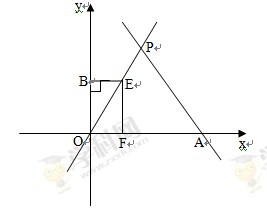
(1)求點(diǎn)P的坐標(biāo);
(2)請(qǐng)判斷△OPA的形狀并說(shuō)明理由;
(3)請(qǐng)?zhí)骄縎與t之間的函數(shù)關(guān)系式,并指出t的取值范圍.
(1)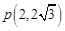 ;
;
(2)等邊三角形;理由見(jiàn)解析;
(3) .
.
解析試題分析:(1)由兩直線相交可列出方程組,求出P點(diǎn)坐標(biāo);
(2)將y=0代入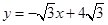 ,可求出OA=4,作PD⊥OA于D,則OD=2,PD=
,可求出OA=4,作PD⊥OA于D,則OD=2,PD=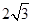 ,利用tan∠POA=
,利用tan∠POA=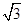 ,可知∠POA=60°,由OP=4.可知△POA是等邊三角形;
,可知∠POA=60°,由OP=4.可知△POA是等邊三角形;
(3)①當(dāng)0<t≤4時(shí),在Rt△EOF中,∠EOF=60°,OE=t,則EF=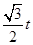 ,OF=
,OF= ,則S=
,則S=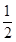 •OF•EF=
•OF•EF= ;
;
②當(dāng)4<t<8時(shí),設(shè)EB與OP相交于點(diǎn)C,易知:CE=PE=t﹣4,AE=8﹣t,可得AF=4﹣ ,EF=
,EF=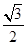 (8﹣t),有OF=OA﹣AF=4﹣(4﹣
(8﹣t),有OF=OA﹣AF=4﹣(4﹣ )=
)= ,S=
,S=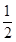 (CE+OF)•EF=﹣
(CE+OF)•EF=﹣ +4
+4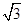 t﹣8
t﹣8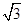 .
.
試題解析:(1)由題意可得: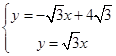 ,
,
解得 ,
,
所以點(diǎn)P的坐標(biāo)為(2,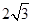 );
);
(2)將y=0代入y=﹣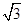 x+4
x+4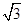 ,得到:﹣
,得到:﹣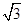 x+4
x+4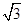 =0,
=0,
∴x=4,即OA=4,
作PD⊥OA于D,則OD=2,PD=2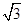 ,
,
∵tan∠POA= =
=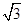 ,
,
∴∠POA=60°,
∵OP= ,
,
∴△POA是等邊三角形;
(3)①當(dāng)0<t≤4時(shí),如圖,在Rt△EOF中,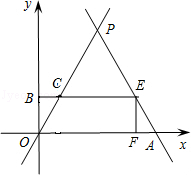
∵∠EOF=60°,OE=t,
∴EF=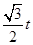 ,OF=
,OF= ,
,
∴S=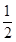 •OF•EF=
•OF•EF= .
.
②當(dāng)4<t<8時(shí),如圖,設(shè)EB與OP相交于點(diǎn)C,
∵CE=PE=t﹣4,AE=8﹣t,
∴AF=4﹣ ,EF=
,EF=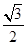 (8﹣t),
(8﹣t),
∴OF=OA﹣AF=4﹣(4﹣ )=
)= ,
,
∴S=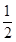 (CE+OF)•EF=
(CE+OF)•EF=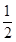 (t﹣4+
(t﹣4+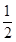 t)×
t)×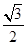 (8﹣t)=
(8﹣t)= 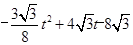 .
.
考點(diǎn):一次函數(shù)綜合題.


 互動(dòng)英語(yǔ)系列答案
互動(dòng)英語(yǔ)系列答案 名牌學(xué)校分層周周測(cè)系列答案
名牌學(xué)校分層周周測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,拋物線過(guò)x軸上兩點(diǎn)A(9,0),C(-3,0),且與y軸交于點(diǎn)B(0,-12).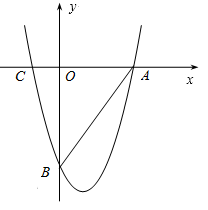
(1)求拋物線的解析式;
(2)若動(dòng)點(diǎn)P從點(diǎn)A出發(fā),以每秒2個(gè)單位沿射線AC方向運(yùn)動(dòng);同時(shí),點(diǎn)Q從點(diǎn)B出發(fā),以每秒1個(gè)單位沿射線BA方向運(yùn)動(dòng),當(dāng)點(diǎn)P到達(dá)點(diǎn)C處時(shí),兩點(diǎn)同時(shí)停止運(yùn)動(dòng).問(wèn)當(dāng)t為何值時(shí),△APQ∽△AOB?
(3)若M為線段AB上一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)M作MN平行于y軸交拋物線于點(diǎn)N.
①是否存在這樣的點(diǎn)M,使得四邊形OMNB恰為平行四邊形?若存在,求出點(diǎn)M的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
②當(dāng)點(diǎn)M運(yùn)動(dòng)到何處時(shí),四邊形CBNA的面積最大?求出此時(shí)點(diǎn)M的坐標(biāo)及四邊形CBNA面積的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
已知二次函數(shù) .
.
(1)求頂點(diǎn)坐標(biāo)和對(duì)稱(chēng)軸方程;
(2)求該函數(shù)圖象與x標(biāo)軸的交點(diǎn)坐標(biāo);
(3)指出x為何值時(shí), ;當(dāng)x為何值時(shí),
;當(dāng)x為何值時(shí), .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,在平面直角坐標(biāo)系中,拋物線經(jīng)過(guò)點(diǎn)A的坐標(biāo)為(m,m),點(diǎn)B的坐標(biāo)為(n,-n),且經(jīng)過(guò)原點(diǎn)O,連接OA、OB、AB,線段AB交y軸于點(diǎn)C.已知實(shí)數(shù)m,n(m<n)分別是方程x2-2x-3=0的兩根.
(1)求m,n的值.
(2)求拋物線的解析式.
(3)若點(diǎn)P為線段OB上的一個(gè)動(dòng)點(diǎn)(不與點(diǎn)O、B重合),直線PC與拋物線交于D、E兩點(diǎn)(點(diǎn)D在y軸右側(cè)),連接OD,BD.當(dāng)△OPC為等腰三角形時(shí),求點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,一條拋物線經(jīng)過(guò)原點(diǎn)和點(diǎn)C(8,0),A、B是該拋物線上的兩點(diǎn),AB∥x軸,OA=5,AB=2.點(diǎn)E在線段OC上,作∠MEN=∠AOC,使∠MEN的一邊始終經(jīng)過(guò)點(diǎn)A,另一邊交線段BC于點(diǎn)F,連接AF.
(1)求拋物線的解析式;
(2)當(dāng)點(diǎn)F是BC的中點(diǎn)時(shí),求點(diǎn)E的坐標(biāo);
(3)當(dāng)△AEF是等腰三角形時(shí),求點(diǎn)E的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
已知二次函數(shù) 為常數(shù),且
為常數(shù),且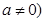 .
.
(1)求證:不論 為何值,該函數(shù)的圖象與
為何值,該函數(shù)的圖象與 軸總有兩個(gè)公共點(diǎn);
軸總有兩個(gè)公共點(diǎn);
(2)設(shè)該函數(shù)的圖象的頂點(diǎn)為C,與 軸交于A,B兩點(diǎn),當(dāng)△ABC的面積等于2時(shí),求
軸交于A,B兩點(diǎn),當(dāng)△ABC的面積等于2時(shí),求 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
已知點(diǎn) 和點(diǎn)
和點(diǎn) 在拋物線
在拋物線 上.
上. 
(1)求 的值及點(diǎn)
的值及點(diǎn) 的坐標(biāo);
的坐標(biāo);
(2)點(diǎn)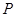 在
在 軸上,且滿(mǎn)足△
軸上,且滿(mǎn)足△ 是以
是以 為直角邊的直角三角形,求點(diǎn)
為直角邊的直角三角形,求點(diǎn)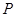 的坐標(biāo);
的坐標(biāo);
(3)平移拋物線 ,記平移后點(diǎn)A的對(duì)應(yīng)點(diǎn)為
,記平移后點(diǎn)A的對(duì)應(yīng)點(diǎn)為 ,點(diǎn)B的對(duì)應(yīng)點(diǎn)為
,點(diǎn)B的對(duì)應(yīng)點(diǎn)為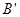 . 點(diǎn)M(2,0)在x軸上,當(dāng)拋物線向右平移到某個(gè)位置時(shí),
. 點(diǎn)M(2,0)在x軸上,當(dāng)拋物線向右平移到某個(gè)位置時(shí), 最短,求此時(shí)拋物線的函數(shù)解析式.
最短,求此時(shí)拋物線的函數(shù)解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
已知拋物線 的頂點(diǎn)在x軸上,且與y軸交于A點(diǎn). 直線
的頂點(diǎn)在x軸上,且與y軸交于A點(diǎn). 直線 經(jīng)過(guò)A、B兩點(diǎn),點(diǎn)B的坐標(biāo)為(3,4).
經(jīng)過(guò)A、B兩點(diǎn),點(diǎn)B的坐標(biāo)為(3,4).
(1)求拋物線的解析式,并判斷點(diǎn)B是否在拋物線上;
(2)如果點(diǎn)B在拋物線上,P為線段AB上的一個(gè)動(dòng)點(diǎn)(點(diǎn)P與A、B不重合),過(guò)P作x軸的垂線與這個(gè)二次函數(shù)的圖象交于點(diǎn)E,設(shè)線段PE的長(zhǎng)為h,點(diǎn)P的橫坐標(biāo)為x.當(dāng)x為何值時(shí),h取得最大值,求出這時(shí)的h值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
如圖,黎叔叔想用60m長(zhǎng)的籬笆靠墻MN圍成一個(gè)矩形花圃ABCD,已知墻長(zhǎng)MN=30m.
(1)能否使矩形花圃ABCD的面積為400m2?若能,請(qǐng)說(shuō)明圍法;若不能,請(qǐng)說(shuō)明理由.
(2)請(qǐng)你幫助黎叔叔設(shè)計(jì)一種圍法,使矩形花圃ABCD的面積最大,并求出最大面積.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com