Question

△ABC是等邊三角形，P為平面內一個動點，BP=BA，若0°＜∠PBC＜180°，且∠PBC的平分線上一點D滿足DB=DA，
（1）當BP和BA重合時（如圖1），∠BPD=______；
（2）當BP在∠ABC內部時（如圖2），求∠BPD；
（3）當BP在∠ABC外部時，請直接寫出∠BPD，并畫出相應的圖形．

Answer 1

解：（1）∠BPD=30°；

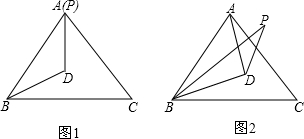
（2）如圖，連接CD，
∵點D在∠PBC的平分線上
∴∠PBD=∠CBD
∵△ABC是等邊三角形
∴BA=BC=AC，∠ACB=60°
∵BP=BA
∴BP=BC
∵BD=BD
∴△PBD≌△CBD（SAS）
∴∠BPD=∠BCD
∵DB=DA，BC=AC，CD=CD
∴△BCD≌△ACD
∴∠BCD=∠ACD=∠ACB=30°
∴∠BPD=30°；

（3）∠BPD=30°或150°圖形如下：
分析：（1）由于P，A重合，DP=DB，∠DBP=∠DPB，因為DB是∠PBC的平分線，因此，∠DBP=∠DPB=30°；
（2）本題可通過構建全等三角形來求解．連接CD，BP=BC，BD又是∠PBC的平分線，三角形PBD和三角形CBD中又有一公共邊，因此兩三角形全等，∠BPD=∠BCD，那么關鍵是求∠BCD的值，那么我們就要看∠BCD和∠ACB的關系了，可通過證明三角形ACD和BCD全等來得出，這兩個三角形中，BD=AD，BC=AC，有一條公共邊CD因此∠BCD=∠ACD=30°，那么就求出∠BPD的度數了；
（3）同（2）的證法完全一樣，步驟有2個，一是得出∠BCD的度數，二是證明三角形BPD和BCD全等，同（2）完全一樣．
（當∠BPD是鈍角時，∠BPD=∠BCD=（360-60）÷2=150°，還是用的（2）中的三角形BPD，BCD全等，BCD，ACD全等）
點評：本題考查了等邊三角形的性質及全等三角形的判定與性質；通過全等三角形得出角相等是解題的關鍵．