
已知:拋物線![]() 與
與![]() 軸的兩個交點(diǎn)分別為A、B,點(diǎn)A在點(diǎn)B的左側(cè),與y軸交于點(diǎn)C,頂點(diǎn)為D,直線
軸的兩個交點(diǎn)分別為A、B,點(diǎn)A在點(diǎn)B的左側(cè),與y軸交于點(diǎn)C,頂點(diǎn)為D,直線![]() 經(jīng)過點(diǎn)A、C.
經(jīng)過點(diǎn)A、C.
1.(1)求點(diǎn)D的坐標(biāo)和直線AC的解析式;
2.(2)點(diǎn)![]() 為拋物線上的一個動點(diǎn),求使得
為拋物線上的一個動點(diǎn),求使得![]() 的面積與
的面積與![]() 的面積相等的點(diǎn)
的面積相等的點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
1.(1)由拋物線解析式![]() ,
,
得D(-1,-4).--------------------------1分
點(diǎn)A、C的坐標(biāo)分別是A(-3,0),C(0,-3),
∵直線![]() 經(jīng)過A、C兩點(diǎn),
經(jīng)過A、C兩點(diǎn),
![]()
![]()
∴ 直線AC的解析式為![]() .----------3分
.----------3分
2.(2)①過點(diǎn)D作與直線![]() 平行的直線,交拋物線于點(diǎn)P.
平行的直線,交拋物線于點(diǎn)P. 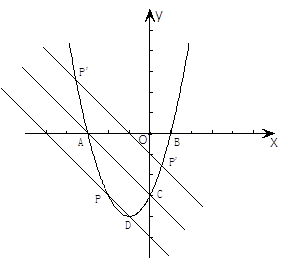
則![]() .
.
設(shè)直線DP的解析式為![]() ,
,
∵ 點(diǎn)D的坐標(biāo)為(-1,-4).∴ t=-5.
∴P(m,-m-5),∴ ![]() ,
,
解得 m=-1(舍去)或m=-2.
∴ P(-2,-3). -----------------------------------------------------6分
②直線DP: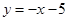 與y軸的交點(diǎn)坐標(biāo)為(0,-5),則直線DP關(guān)于直線
與y軸的交點(diǎn)坐標(biāo)為(0,-5),則直線DP關(guān)于直線![]() 對稱的直線
對稱的直線![]() 的解析式為
的解析式為![]() ,
,![]() 交拋物線于P’,設(shè)P’(m’,-m’-1).
交拋物線于P’,設(shè)P’(m’,-m’-1).
由于點(diǎn)P’在拋物線![]() 上,∴
上,∴ ![]() .
.
解得 ![]() ------------------------------------7分
------------------------------------7分
∴ P’( )或P’(
)或P’(![]() ). --------------8分
). --------------8分
∴ 所求點(diǎn)![]() 的坐標(biāo)分別是(-2,-3),(
的坐標(biāo)分別是(-2,-3),(![]() ),(
),(![]() )
)
解析:略



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
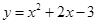 與
與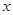 軸的兩個交點(diǎn)分別為A、B,點(diǎn)A在點(diǎn)B的左側(cè),與y軸交于點(diǎn)C,頂點(diǎn)為D,直線
軸的兩個交點(diǎn)分別為A、B,點(diǎn)A在點(diǎn)B的左側(cè),與y軸交于點(diǎn)C,頂點(diǎn)為D,直線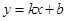 經(jīng)過點(diǎn)A、C.
經(jīng)過點(diǎn)A、C.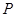 為拋物線上的一個動點(diǎn),求使得
為拋物線上的一個動點(diǎn),求使得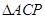 的面積與
的面積與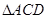 的面積相等的點(diǎn)
的面積相等的點(diǎn)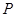 的坐標(biāo).
的坐標(biāo).查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2011-2012年北京市華夏女子中學(xué)九年級第一學(xué)期期中考試數(shù)學(xué)卷 題型:解答題
已知:拋物線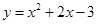 與
與 軸的兩個交點(diǎn)分別為A、B,點(diǎn)A在點(diǎn)B的左側(cè),與y軸交于點(diǎn)C,頂點(diǎn)為D,直線
軸的兩個交點(diǎn)分別為A、B,點(diǎn)A在點(diǎn)B的左側(cè),與y軸交于點(diǎn)C,頂點(diǎn)為D,直線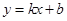 經(jīng)過點(diǎn)A、C.
經(jīng)過點(diǎn)A、C.
【小題1】(1)求點(diǎn)D的坐標(biāo)和直線AC的解析式;
【小題2】(2)點(diǎn)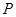 為拋物線上的一個動點(diǎn),求使得
為拋物線上的一個動點(diǎn),求使得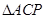 的面積與
的面積與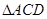 的面積相等的點(diǎn)
的面積相等的點(diǎn)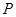 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2013-2014學(xué)年北京市海淀區(qū)九年級第一學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:解答題
已知拋物線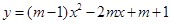 (
(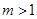 ).
).
(1)求拋物線與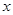 軸的交點(diǎn)坐標(biāo);
軸的交點(diǎn)坐標(biāo);
(2)若拋物線與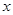 軸的兩個交點(diǎn)之間的距離為2,求
軸的兩個交點(diǎn)之間的距離為2,求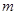 的值;
的值;
(3)若一次函數(shù)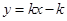 的圖象與拋物線始終只有一個公共點(diǎn),求一次函數(shù)的解析式.
的圖象與拋物線始終只有一個公共點(diǎn),求一次函數(shù)的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2011-2012年北京市九年級第一學(xué)期期中考試數(shù)學(xué)卷 題型:解答題
已知:拋物線 與
與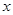 軸的兩個交點(diǎn)分別為A、B,點(diǎn)A在點(diǎn)B的左側(cè),與y軸交于點(diǎn)C,頂點(diǎn)為D,直線
軸的兩個交點(diǎn)分別為A、B,點(diǎn)A在點(diǎn)B的左側(cè),與y軸交于點(diǎn)C,頂點(diǎn)為D,直線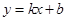 經(jīng)過點(diǎn)A、C.
經(jīng)過點(diǎn)A、C.
1.(1)求點(diǎn)D的坐標(biāo)和直線AC的解析式;
2.(2)點(diǎn) 為拋物線上的一個動點(diǎn),求使得
為拋物線上的一個動點(diǎn),求使得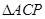 的面積與
的面積與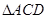 的面積相等的點(diǎn)
的面積相等的點(diǎn) 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com