
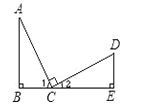
【題目】已知:如圖所示,AC=CD,∠B=∠E=90°,AC⊥CD,則不正確的結論是( )
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A與∠D互為余角
【答案】A
【解析】試題分析:A選項:因為AC⊥CD,∠ACD=90°,所以可得:∠1+∠2=90°,所以A選項錯誤;
B選項:因為AC⊥CD,∠ACD=90°,所以可得:∠1+∠2=90°,又因為∠B=90°,所以∠1+∠A=90°,根據同角的余角相等可得:∠A=∠2,故B選項正確;
C選項:因為AC⊥CD,∠ACD=90°,所以可得:∠1+∠2=90°,又因為∠B=90°,所以∠1+∠A=90°,根據同角的余角相等可得:∠A=∠2,又因為AC=CD,∠B=∠E,根據AAS可證△ABC≌△CED,故C選項正確;
D選項:因為AC⊥CD,∠ACD=90°,所以可得:∠1+∠2=90°,又因為∠B=90°,所以∠1+∠A=90°,根據同角的余角相等可得:∠A=∠2,因為∠E=90°,所以∠D+∠2=90°,所以∠A+∠D=90°,所以∠A和∠D互為余角,故D選項正確.
故應選A.


科目:初中數學 來源: 題型:
【題目】在某校九年級安全疏散演習中,各班疏散的時間分別是3分,2分40秒,3分20秒,3分30秒,2分45秒,這次演習中,疏散時間的極差為____秒.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB∥CD,C在D的右側,BE平分∠ABC,DE平分∠ADC,BE、DE所在直線交于點E.∠ADC =70°.

(1)求∠EDC的度數;
(2)若∠ABC =n°,求∠BED的度數(用含n的代數式表示);
(3)將線段BC沿DC方向平移, 使得點B在點A的右側,其他條件不變,畫出圖形并判斷∠BED的度數是否改變,若改變,求出它的度數(用含n的式子表示),不改變,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列事件中,是隨機事件的是( )
A. 通常加熱到100℃時,水沸騰 B. 度量三角形的外角和,結果是360°
C. 明天太陽從西邊升起 D. 籃球隊員在罰球線上投籃一次,未投中
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用配方法解一元二次方程x2+4x﹣5=0,此方程可變形為( )
A.(x+2)2=9
B.(x﹣2)2=9
C.(x+2)2=1
D.(x﹣2)2=1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com