
【題目】已知:數軸上A、B兩點表示的有理數分別為a、b,且(a﹣1)2+|b+2|=0
(1)求(a+b)2017的值.
(2)數軸上的點C與A、B兩點的距離的和為7,求點C在數軸上表示的數c的值.
![]()
【答案】(1)﹣1;(2)﹣4或3.
【解析】試題分析:
(1)由已知條件可得![]() 的值,代入
的值,代入![]() 中計算即可;
中計算即可;
(2)由(1)可知A、B兩點間的距離為3,因此點C不在A、B之間,可分點C在A的右側和點C在B的左側兩種情形結合圖形討論即可得到答案.
試題解析:
(1)∵(a﹣1)2+|b+2|=0,
∴ a﹣1=0,b+2=0,
解得a=1,b=﹣2,
∴(a+b)2017=(1﹣2)2017=(﹣1)2017=﹣1;
(2)∵a=1,b=﹣2,數軸上A、B兩點表示的有理數分別為a、b,數軸上的點C與A、B兩點的距離的和為7,
∴點C可能在點B的左側或點C可能在點A的右側,
當點C在點B的左側時,1﹣c+﹣2﹣c=7,得c=﹣4,
當點C在點A的右側時,c﹣1+c﹣(﹣2)=7,得c=3.


科目:初中數學 來源: 題型:
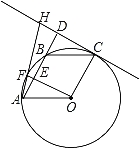
【題目】(2016湖北省荊州市第23題)如圖,A、F、B、C是半圓O上的四個點,四邊形OABC是平行四邊形,∠FAB=15°,連接OF交AB于點E,過點C作OF的平行線交AB的延長線于點D,延長AF交直線CD于點H.
(1)求證:CD是半圓O的切線;
(2)若DH=6﹣3![]() ,求EF和半徑OA的長.
,求EF和半徑OA的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在數軸上A點表示數a,B點示數b,C點表示數c,b是最小的正整數,且a,c滿足![]() +(c-8)2=0.
+(c-8)2=0.
![]()
(1) a = ,b = ,c = .
(2) 若將數軸折疊,使得A點與B點重合,則點C與數 表示的點重合.
(3) 點A,B,C開始在數軸上運動,若點A以每秒2個單位長度的速度向左運動,同時,點B和點C分別以每秒4個單位長度和8個單位長度的速度向右運動,假設t秒鐘過后,若點A與點B之間的距離表示為AB,點A與點C之間的距離表示為AC,點B與點C之間的距離表示為BC.則AB = ,AC = ,BC = .(用含t的代數式表示)
(4) 請問:3AB-(2BC+AC)的值是否隨著時間t的變化而改變? 若變化,請說明理由;若不變,請求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛貨車從百貨大樓出發負責送貨,向東走了4千米到達小明家,繼續向東走了1.5千米到達小紅家,然后向西走了8.5千米到達小剛家,最后返回百貨大樓.

(1)以百貨大樓為原點,向東為正方向,1個單位長度表示1千米,請你在數軸上標出小明、小紅、小剛家的位置.(小明家用點A表示,小紅家用點B表示,小剛家用點C表示)
(2)小明家與小剛家相距多遠?
(3)若貨車每千米耗油1.5升,那么這輛貨車此次送貨共耗油多少升
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】團隊游客年齡的方差分別是S甲2=1.4,S乙2=18.8,S丙2=2.5,導游小力最喜歡帶游客年齡相近齡的團隊,則他在甲、乙、丙三個的中應選_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】合肥百大集團新進了40臺空調機,60臺電冰箱,計劃調配給下屬的甲、乙兩個連鎖店銷售,其中70臺給甲連鎖店,30臺給乙連鎖店.兩個連鎖店銷售這兩種電器每臺的利潤(元)如下表:
空調機 | 電冰箱 | |
甲連鎖店 | 200 | 170 |
乙連鎖店 | 160 | 150 |
設集團調配給甲連鎖店x臺空調機,集團賣出這100臺電器的總利潤為y(元).
(1)求y關于x的函數關系式,并求出x的取值范圍;
(2)為了促銷,集團決定僅對甲連鎖店的空調機每臺讓利a元銷售,其他的銷售利潤不變,并且讓利后每臺空調機的利潤仍然高于甲連鎖店銷售的每臺電冰箱的利潤,問該集團應該如何設計調配方案,才能使總利潤達到最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘數學家把1,3,6,10,15,21叫做三角數,它有一定的規律性,若把第一個三角數記為a1,第二個三角數記為a2,, 第n個三角數記為an,計算a1+a2,a2+a3,a3+a4,,由此推算a199+a200的值為( )
A. 20000 B. 40000 C. 39701 D. 19701
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com