
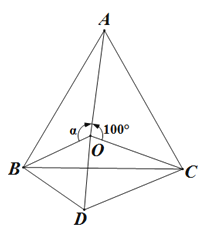
【題目】如圖,點O是等邊△ABC內一點,∠AOC=100°,∠AOB=α,以OB為邊作等邊△BOD,連接CD.
(1)求證:△ABO≌△CBD;
(2)當α=150°時,試判斷△COD的形狀,并說明理由;
(3)探究:當α為多少度時△COD是等腰三角形?
【答案】(1)詳見解析;(2)直角三角形,理由詳見解析;(3)當α為100°、130°、160°時,△COD是等腰三角形.
【解析】
(1)由于 △ABC和△OBD都是等邊三角形,可得BA=BC,BO=BD,由角推出∠ABO=∠CBD,即可證明△ABO≌△CBD.
(2)由△ABO≌△CBD,可得∠BDC=150°,由于∠BDO=60°,即可推出∠CDO的度數為90°,即可證明為直角三角形.
(3)分三類討論:①要使CO=CD, ②要使OC=OD,③要使OD=CD.
(1)解:(1)∵△ABC和△OBD都是等邊三角形,
∴BA=BC,BO=BD,
∵∠ABC=∠OBD=60°
∴∠ABO=∠CBD,
∴△ABO≌△CBD(SAS).
(2)直角三角形;
理由:∵△ABO≌△CBD
∴∠BDC=∠AOB=150°
又∵∠ODB=∠OBD=60°
∴∠CDO=150°-60°=90°
∴△COD是直角三角形.
(3)①要使CO=CD,需∠COD=∠CDO,
∴200°-α = α-60°,
∴α=130°;
②要使OC=OD,需∠OCD=∠CDO,
∴2(α-60°)=180°-(200°-α),
∴α=100°;
③要使OD=CD,需∠OCD=∠COD,
∴2(200°-α)=180°-(α -60°),
∴α=160°.
所以當α為100°、130°、160°時,△COD是等腰三角形.


科目:初中數學 來源: 題型:
【題目】我們知道:在小學已經學過“正方形的四條邊都相等,正方形的四個內角都是直角”,試利用上述知識,并結合已學過的知識解答下列問題:
如圖1,在正方形ABCD中,G是射線DB上的一個動點(點G不與點D重合),以CG為邊向下作正方形CGEF.
(1)當點G在線段BD上時,求證:![]() ;
;
(2)連接BF,試探索:BF,BG與AB的數量關系,并說明理由;
(3)若AB=a(a是常數),如圖2,過點F作FT∥BC,交射線DB于點T,問在點G的運動過程中,GT的長度是否會隨著G點的移動而變化?若不變,請求出GT的長度;若變化,請說明理由.
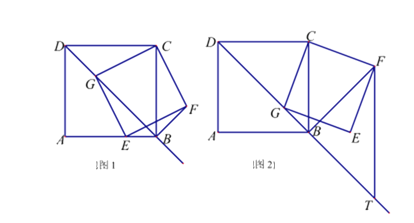
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,CD切⊙O于點C,與BA的延長線交于點D,OE⊥AB交⊙O于點E,連接CA、CE、CB,CE交AB于點G,過點A作AF⊥CE于點F,延長AF交BC于點P.
(Ⅰ)求∠CPA的度數;
(Ⅱ)連接OF,若AC=![]() ,∠D=30°,求線段OF的長.
,∠D=30°,求線段OF的長.
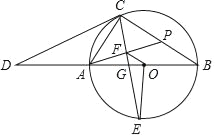
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,點D是半圓O上一點,點C是![]() 的中點,CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE、CB于點P、Q,連接AC.
的中點,CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE、CB于點P、Q,連接AC.
(1)求證:GP=GD;
(2)求證:P是線段AQ的中點;
(3)連接CD,若CD=2,BC=4,求⊙O的半徑和CE的長.
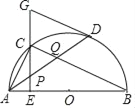
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC=AC=20 cm.動點P,Q分別從A,B兩點同時出發,沿三角形的邊勻速運動.已知點P,點Q的速度都是2 cm/s,當點P第一次到達B點時,P,Q兩點同時停止運動.設點P的運動時間為t(s).
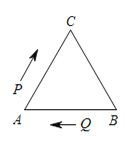
(1)∠A=______度;
(2)當0<t<10,且△APQ為直角三角形時,求t的值;
(3)當△APQ為等邊三角形時,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
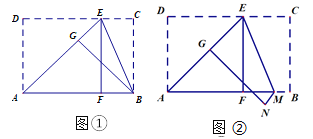
【題目】李剛和常明兩人在數學活動課上進行折紙創編活動.李剛拿起一張準備好的長方形紙片對常明說:“我現在折疊紙片(圖①),使點D落在AB邊的點F處,得折痕AE,再折疊,使點C落在AE邊的點G處,此時折痕恰好經過點B,如果AD=![]() ,那么AB長是多少?”常明說;“簡單,我會. AB應該是_____”.
,那么AB長是多少?”常明說;“簡單,我會. AB應該是_____”.
常明回答完,又對李剛說:“你看我的創編(圖②),與你一樣折疊,可是第二次折疊時,折痕不經過點B,而是經過了AB邊上的M點,如果AD=![]() ,測得EC=3BM,那么AB長是多少?”李剛思考了一會,有點為難,聰明的你,你能幫忙解答嗎?AB=_____.
,測得EC=3BM,那么AB長是多少?”李剛思考了一會,有點為難,聰明的你,你能幫忙解答嗎?AB=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC在直角坐標平面內,三個頂點的坐標分別為A(0,3)、B(3,4)、C(2,2)(正方形網格中每個小正方形的邊長是一個單位長度).
(1)畫出△ABC向下平移4個單位長度得到的△A1B1C1,點C1的坐標是 ;
(2)以點B為位似中心,在網格內畫出△A2B2C2,使△A2B2C2與△ABC位似,且位似比為2:1;
(3)四邊形AA2C2C的面積是 平方單位.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+2ax+3a2+3(其中x是自變量),當x≥2時,y隨x的增大而增大,且2≤x≤1時,y的最大值為9,則a的值為
A. 1或2 B. ![]() 或
或![]()
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,![]() 、
、![]() 、
、![]() .
.
(1)請畫出![]() 關于
關于![]() 軸對稱的
軸對稱的![]() (其中
(其中![]() 、
、![]() 、
、![]() 分別是
分別是![]() 、
、![]() 、
、![]() 的對應點)并直接寫出
的對應點)并直接寫出![]() 點的坐標為 .
點的坐標為 .
(2)若直線![]() 經過點
經過點![]() 且與
且與![]() 軸平行,則點
軸平行,則點![]() 關于直線
關于直線![]() 的對稱點的坐標為 .
的對稱點的坐標為 .
(3)在![]() 軸上存在一點
軸上存在一點![]() ,使
,使![]() 最大,則點
最大,則點![]() 的坐標為 .
的坐標為 .
(4)第一象限有一點![]() ,在
,在![]() 軸上找一點
軸上找一點![]() 使
使![]() 最短,畫出最短路徑,保留作圖跡.
最短,畫出最短路徑,保留作圖跡.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com