
【題目】已知拋物線![]() .
.
(1)當(dāng)頂點(diǎn)坐標(biāo)為![]() 時(shí),求拋物線的解析式;
時(shí),求拋物線的解析式;
(2)當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 是拋物線圖象上的兩點(diǎn),且
是拋物線圖象上的兩點(diǎn),且![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若拋物線上的點(diǎn)![]() ,滿足
,滿足![]() 時(shí),
時(shí),![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() ;(3)
;(3) ![]() 或
或![]()
【解析】分析:(1)利用拋物線的頂點(diǎn)坐標(biāo)公式即可得出結(jié)論;
(2)先確定出拋物線對(duì)稱(chēng)軸x=﹣1,進(jìn)而得出點(diǎn)Q的坐標(biāo),即可得出結(jié)論;
(3)分三種情況利用拋物線的增減性建立方程組即可得出結(jié)論.
詳解:(1)由已知得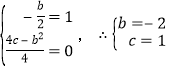 ,
,
∴拋物線的解析式為 y=x2﹣2x+1;
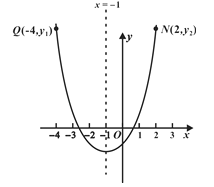
(2)當(dāng)b=2時(shí),y=x2+2x+c, ∴對(duì)稱(chēng)軸直線x=﹣1.
由圖取拋物線上點(diǎn)Q,使Q與N關(guān)于對(duì)稱(chēng)軸x=﹣1對(duì)稱(chēng),由N(2,y2)得Q(﹣4,y2).
又∵M(m,y1)在拋物線圖象上的點(diǎn),且y1>y2,由函數(shù)增減性得:m<﹣4或m>2;
(3)分三種情況:
①當(dāng)﹣![]() <﹣1,即b>2時(shí),函數(shù)值y隨x的增大而增大,依題意有:
<﹣1,即b>2時(shí),函數(shù)值y隨x的增大而增大,依題意有:![]()
②當(dāng)﹣1≤﹣![]() ≤1,即﹣2≤b≤2時(shí),x=﹣
≤1,即﹣2≤b≤2時(shí),x=﹣![]() 時(shí),函數(shù)值y取最小值,分兩種情況討論:
時(shí),函數(shù)值y取最小值,分兩種情況討論:
(ⅰ)若0≤﹣![]() ≤1,即﹣2≤b≤0時(shí),依題意有:
≤1,即﹣2≤b≤0時(shí),依題意有:
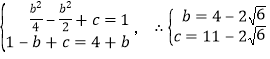 或
或![]() (舍去)
(舍去)
(ⅱ)若﹣1≤﹣![]() ≤0,即0≤b≤2時(shí),依題意有
≤0,即0≤b≤2時(shí),依題意有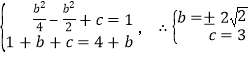 (舍去)
(舍去)
③當(dāng)﹣![]() >1,即b<﹣
>1,即b<﹣![]() (舍去)
(舍去)
綜上所述:![]() 或
或![]() .
.


 導(dǎo)學(xué)與測(cè)試系列答案
導(dǎo)學(xué)與測(cè)試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形OABC為矩形,以點(diǎn)O為原點(diǎn)建立直角坐標(biāo)系,點(diǎn)C在x軸的正半軸上,點(diǎn)A在y軸的正半軸上,反比例函數(shù)y=![]() 圖象經(jīng)過(guò)AB的中點(diǎn)D(1,3),且與BC交于點(diǎn)E,設(shè)直線DE的解析式為y=mx+n.
圖象經(jīng)過(guò)AB的中點(diǎn)D(1,3),且與BC交于點(diǎn)E,設(shè)直線DE的解析式為y=mx+n.
(1)求k的值和點(diǎn)E的坐標(biāo);
(2)直接寫(xiě)出不等式![]() -n>mx的解集;
-n>mx的解集;
(3)點(diǎn)Q為x軸上一點(diǎn),點(diǎn)P為反比例函數(shù)y=![]() 圖象上一點(diǎn),是否存在點(diǎn)P、Q,使得以P、Q、D、E為頂點(diǎn)的四邊形為平行四邊形?如果存在,請(qǐng)直接寫(xiě)出點(diǎn)P的坐標(biāo);如果不存在,請(qǐng)說(shuō)明理由.
圖象上一點(diǎn),是否存在點(diǎn)P、Q,使得以P、Q、D、E為頂點(diǎn)的四邊形為平行四邊形?如果存在,請(qǐng)直接寫(xiě)出點(diǎn)P的坐標(biāo);如果不存在,請(qǐng)說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)x、y是任意兩個(gè)有理數(shù),規(guī)定x與y之間的一種運(yùn)算“⊕”為:
x⊕y=![]()
(1)試求1⊕(-1)的值;
(2)試判斷該運(yùn)算“⊕”是否具有交換律,說(shuō)明你的理由;
(3)若2⊕x=0,求x的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某電器超市銷(xiāo)售每臺(tái)進(jìn)價(jià)為120元、170元的A,B兩種型號(hào)的電風(fēng)扇,如表所示是近2周的銷(xiāo)售情況:(進(jìn)價(jià)、售價(jià)均保持不變,利潤(rùn)=銷(xiāo)售收入一進(jìn)貨成本)
銷(xiāo)售時(shí)段 | 銷(xiāo)售數(shù)量 | 銷(xiāo)售收入 | |
A種型號(hào) | B種型號(hào) | ||
第一周 | 6 | 5 | 2200元 |
第二周 | 4 | 10 | 3200元 |
(1)求A、B兩種型號(hào)的電風(fēng)扇的銷(xiāo)售單價(jià);
(2)若超市再采購(gòu)這兩種型號(hào)的電風(fēng)扇共130臺(tái),并且全部銷(xiāo)售完,該超市能否實(shí)現(xiàn)這兩批的總利潤(rùn)為8010元的目標(biāo)?若能,請(qǐng)給出相應(yīng)的采購(gòu)方案;若不能,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】 觀察下列三行數(shù):
2,4,8,16,32,![]()
![]() ,1,2,4,8,
,1,2,4,8,![]()
1,5,7,17,31,![]()
如圖,第一行數(shù)的第n(n為正整數(shù))個(gè)數(shù)![]() 用來(lái)表示,第二行數(shù)的第n個(gè)數(shù)用
用來(lái)表示,第二行數(shù)的第n個(gè)數(shù)用![]() 來(lái)表示,第三行數(shù)的第n個(gè)數(shù)用
來(lái)表示,第三行數(shù)的第n個(gè)數(shù)用![]() 來(lái)表示
來(lái)表示
(1)根據(jù)你發(fā)現(xiàn)的規(guī)律,請(qǐng)用含n的代數(shù)式表示數(shù)![]() ,
,![]() ,
,![]() 的值
的值![]() = ;
= ; ![]() = ;
= ; ![]() = ;
= ;
(2)取每行的第6個(gè)數(shù),計(jì)算這三個(gè)數(shù)的和
(3)若![]() 記為x,求
記為x,求![]() (結(jié)果用含x的式子表示并化簡(jiǎn))
(結(jié)果用含x的式子表示并化簡(jiǎn))
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,點(diǎn)D、E、F分別是邊AB、AC、BC的中點(diǎn),且BC=2AF。
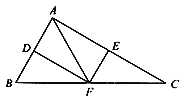
(1)求證:四邊形ADEF為矩形;
(2)若∠C=30°、AF=2,寫(xiě)出矩形ADEF的周長(zhǎng)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)a1=22-02,a2=32-12,…,an=(n+1)2-(n-1)2(n為大于1的整數(shù))
(1)計(jì)算a15的值;
(2)通過(guò)拼圖你發(fā)現(xiàn)前三個(gè)圖形的面積之和與第四個(gè)正方形的面積之間有什么關(guān)系:
__________________________________(用含a、b的式子表示);

(3)根據(jù)(2)中結(jié)論,探究an=(n+1)2-(n-1)2是否為4的倍數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,平面直角坐標(biāo)系中,矩形OABC的兩邊分別在x軸和y軸上,OA=![]() cm,OC=8cm,現(xiàn)有兩動(dòng)點(diǎn)P、Q分別從O、C同時(shí)出發(fā),P在線段OA上沿OA方向以每秒
cm,OC=8cm,現(xiàn)有兩動(dòng)點(diǎn)P、Q分別從O、C同時(shí)出發(fā),P在線段OA上沿OA方向以每秒![]() cm的速度勻速運(yùn)動(dòng),Q在線段CO上沿CO方向以每秒1cm的速度勻速運(yùn)動(dòng).設(shè)運(yùn)動(dòng)時(shí)間為t秒.
cm的速度勻速運(yùn)動(dòng),Q在線段CO上沿CO方向以每秒1cm的速度勻速運(yùn)動(dòng).設(shè)運(yùn)動(dòng)時(shí)間為t秒.
(1)用t的式子表示△OPQ的面積S;
(2)求證:四邊形OPBQ的面積是一個(gè)定值,并求出這個(gè)定值;
(3)當(dāng)△OPQ與△PAB和△QPB相似時(shí),拋物線y=![]() x 2+bx+c經(jīng)過(guò)B、P兩點(diǎn),過(guò)線段BP上一動(dòng)點(diǎn)M作y軸的平行線交拋物線于N,當(dāng)線段MN的長(zhǎng)取最大值時(shí),求直線MN把四邊形OPBQ分成兩部分的面積之比.
x 2+bx+c經(jīng)過(guò)B、P兩點(diǎn),過(guò)線段BP上一動(dòng)點(diǎn)M作y軸的平行線交拋物線于N,當(dāng)線段MN的長(zhǎng)取最大值時(shí),求直線MN把四邊形OPBQ分成兩部分的面積之比.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著人們環(huán)保意識(shí)的增強(qiáng),“低碳出行”越來(lái)越為人們所倡導(dǎo)。小李要從家鄉(xiāng)到寧波工作,若乘飛機(jī)需要3小時(shí),乘汽車(chē)需要9小時(shí)。這兩種交通工具每小時(shí)排放的二氧化碳總量為80千克,已知飛機(jī)每小時(shí)二氧化碳的排放量比汽車(chē)多46千克,若小李乘汽車(chē)來(lái)寧波,那么他此行與乘飛機(jī)相比將減少二氧化碳排放量多少千克?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com