
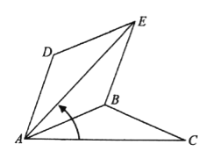
【題目】如圖,在等腰![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() ,得到
,得到![]() ,連結(jié)
,連結(jié)![]() .
.
(1)求證:![]() ;
;
(2)四邊形![]() 是什么形狀的四邊形?并說(shuō)明理由;
是什么形狀的四邊形?并說(shuō)明理由;
(3)直接寫出:當(dāng)![]() 分別是多少度時(shí),①
分別是多少度時(shí),①![]() ;②
;②![]() .
.
【答案】(1)見解析;(2)四邊形ABED是菱形.理由見解析;(3)① α=30°;② α=60°
【解析】
(1)由旋轉(zhuǎn)的性質(zhì)可得∠EAC=2α,∠DAE=∠BAC=α,由“SAS”可證△ABE≌△ABC,可得BE=BC;
(2)由旋轉(zhuǎn)的性質(zhì)可得AD=AB,BC=DE,且AB=BC,BE=BC,可證四邊形ABED是菱形;
(3)由菱形的性質(zhì)可求解.
(1)證明:∵將△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)2![]() ,
,
根據(jù)旋轉(zhuǎn)的性質(zhì)得:
∴∠EAC=2![]() ,∠DAE=∠BAC=
,∠DAE=∠BAC=![]() ,AD=AB,AE=AC,
,AD=AB,AE=AC,
∴∠BAE=∠EAC-∠BAC=2![]() -
-![]() =
=![]() ,
,
∴∠BAE=∠BAC,
∵AE=AC,AB=AB,
∴△ABE≌△ABC(SAS),
∴BE=BC;
(2)答:四邊形ABED是菱形.
理由如下:
∵將△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)2![]() ,
,
∴AD=AB,BC=DE,
∵AB=BC,BE=BC,
∴AD=AB=BE=DE,
∴四邊形ABED是菱形;
(3)如圖,當(dāng)BE⊥AC時(shí),延長(zhǎng)EB交AC于H,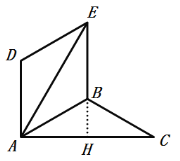
∵四邊形ABED是菱形,
∴AD∥BE,
∵BE⊥AC,
∴AD⊥AC,
∴∠DAC=90°,
∵∠DAE=∠BAC=![]() ,∠EAC=2
,∠EAC=2![]() ,
,
∴![]() +2
+2![]() =90°,
=90°,
∴![]() =30°;
=30°;
如圖,當(dāng)BE∥AC,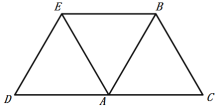
∵四邊形ABED是菱形,
∴AD∥BE,
又∵BE∥AC,
∴AD與AC共線,
∴∠DAE+∠EAC=180°,
∴![]() +2
+2![]() =180°,
=180°,
∴![]() =60°.
=60°.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)經(jīng)過(guò)點(diǎn)A、B,與y軸負(fù)半軸交于點(diǎn)C,且OC=OB,其中B點(diǎn)坐標(biāo)為(3,0),對(duì)稱軸l為直線x=![]() .
.
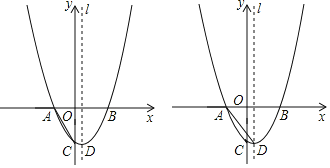
(1)求拋物線的解析式;
(2)在x軸上方有一點(diǎn)P,連接PA后滿足∠PAB=∠CAB,記△PBC的面積為S,求當(dāng)S=10.5時(shí)點(diǎn)P的坐標(biāo);
(3)在(2)的條件下,當(dāng)點(diǎn)P恰好落在拋物線上時(shí),將直線BC上下平移,平移后的直線y=x+t與拋物線交于C′、B′兩點(diǎn)(C′在B′的左側(cè)),若以點(diǎn)C′、B′、P為頂點(diǎn)的三角形是直角三角形,求出t的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(1)問(wèn)題發(fā)現(xiàn)
如圖1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,點(diǎn)D是線段AB上一動(dòng)點(diǎn),連接BE.
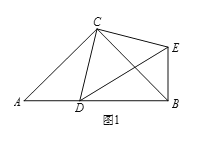
填空: ①![]() 的值為 ;②∠DBE的度數(shù)為 .
的值為 ;②∠DBE的度數(shù)為 .
(2)類比探究
如圖2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,點(diǎn)D是線段AB上一動(dòng)點(diǎn),連接BE.請(qǐng)判斷![]() 的值及∠DBE的度數(shù),并說(shuō)明理由.
的值及∠DBE的度數(shù),并說(shuō)明理由.
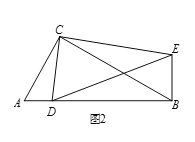
(3)拓展延伸
如面3,在(2)的條件下,將點(diǎn)D改為直線AB上一動(dòng)點(diǎn),其余條件不變,取線段DE的中點(diǎn)M,連接BM、CM,若AC=2,則當(dāng)△CBM是直角三角形時(shí),線段BE的長(zhǎng)是多少?請(qǐng)直接寫出答案.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在扇形AOB中,∠AOB=90°,半徑OA=4.將扇形AOB沿過(guò)點(diǎn)B的直線折疊,點(diǎn)O恰好落在弧AB上點(diǎn)C處,折痕交OA于點(diǎn)D,則圖中陰影部分的面積為_______ .
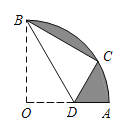
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】連接正八邊形的三個(gè)頂點(diǎn),得到如圖所示的圖形,下列說(shuō)法錯(cuò)誤的是( )

A.四邊形![]() 與四邊形
與四邊形![]() 的面積相等
的面積相等
B.連接![]() ,則
,則![]() 分別平分
分別平分![]() 和
和![]()
C.整個(gè)圖形是軸對(duì)稱圖形,但不是中心對(duì)稱圖形
D.![]() 是等邊三角形
是等邊三角形
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,某校教學(xué)樓![]() 與實(shí)驗(yàn)樓
與實(shí)驗(yàn)樓![]() 的水平間距
的水平間距![]() 米,在實(shí)驗(yàn)樓頂部
米,在實(shí)驗(yàn)樓頂部![]() 點(diǎn)測(cè)得教學(xué)樓頂部
點(diǎn)測(cè)得教學(xué)樓頂部![]() 點(diǎn)的仰角是
點(diǎn)的仰角是![]() ,底部
,底部![]() 點(diǎn)的俯角是
點(diǎn)的俯角是![]() ,則教學(xué)樓
,則教學(xué)樓![]() 的高度是____米(結(jié)果保留根號(hào)).
的高度是____米(結(jié)果保留根號(hào)).
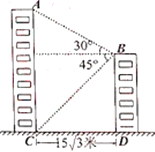
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,四邊形![]() 是矩形,
是矩形,![]() ,將
,將![]() 沿直線
沿直線![]() 翻折,使點(diǎn)
翻折,使點(diǎn)![]() 落在點(diǎn)
落在點(diǎn)![]() 處,
處,![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,若
,若![]() ,則點(diǎn)
,則點(diǎn)![]() 的坐標(biāo)為( )
的坐標(biāo)為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在邊長(zhǎng)為6的菱形ABCD中,對(duì)角線AC,BD交點(diǎn)與點(diǎn)O,點(diǎn)P是△ADO的重心.
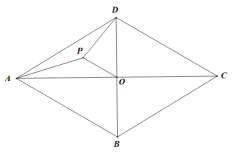
(1)當(dāng)菱形ABCD是正方形時(shí),則PA=________,PD=__________,PO=_________.
(2)線段PA,PD,PO中是否存在長(zhǎng)度保持不變的線段,若存在,請(qǐng)求出該線段的長(zhǎng)度,若不存在,請(qǐng)說(shuō)明理由.
(3)求線段PD,DO滿足的等量關(guān)系,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
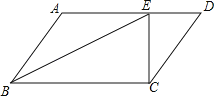
【題目】如圖,在平行四邊形ABCD中,E為AD邊上一點(diǎn),BE平分∠ABC,連接CE,已知DE=6,CE=8,AE=10.
(1)求AB的長(zhǎng);
(2)求平行四邊形ABCD的面積;
(3)求cos∠AEB.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com