
【題目】已知,如圖1,在ABCD中,點E是AB中點,連接DE并延長,交CB的延長線于點F.
(1)求證:△ADE≌△BFE;
(2)如圖2,點G是邊BC上任意一點(點G不與點B、C重合),連接AG交DF于點H,連接HC,過點A作AK∥HC,交DF于點K.
①求證:HC=2AK;
②當點G是邊BC中點時,恰有HD=nHK(n為正整數),求n的值.

【答案】(1)詳見解析;(2)詳見解析;(3)n=4.
【解析】
(1)根據平行四邊形的性質得到AD∥BC,得到∠ADE=∠BFE,∠A=∠FBE,利用AAS定理證明即可;
(2)作BN∥HC交EF于N,根據全等三角形的性質、三角形中位線定理證明;
(3)作GM∥DF交HC于M,分別證明△CMG∽△CHF、△AHD∽△GHF、△AHK∽△HGM,根據相似三角形的性質計算即可.
(1)證明:∵四邊形ABCD是平行四邊形,
∴AD∥BC,
∴∠ADE=∠BFE,∠A=∠FBE,
在△ADE和△BFE中,
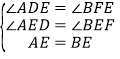
∴△ADE≌△BFE;
(2)如圖2,作BN∥HC交EF于N,

∵△ADE≌△BFE,
∴BF=AD=BC,
∴BN=![]() HC,
HC,
由(1)的方法可知,△AEK≌△BFN,
∴AK=BN,
∴HC=2AK;
(3)如圖3,作GM∥DF交HC于M,

∵點G是邊BC中點,
∴CG=![]() CF,
CF,
∵GM∥DF,
∴△CMG∽△CHF,
∴![]() ,
,
∵AD∥FC,
∴△AHD∽△GHF,
∴![]() ,
,
∴![]() ,
,
∵AK∥HC,GM∥DF,
∴△AHK∽△HGM,
∴![]() ,
,
∴![]() ,即HD=4HK,
,即HD=4HK,
∴n=4.


科目:初中數學 來源: 題型:
【題目】△ABC中,![]() ∠ACB=900,AC=BC,直線MN經過點C,且
∠ACB=900,AC=BC,直線MN經過點C,且![]() AD⊥MN于D,
AD⊥MN于D,![]() BE⊥MN于E.
BE⊥MN于E.
![]() 當直線MN繞點C旋轉到圖1的位置時,求證:
當直線MN繞點C旋轉到圖1的位置時,求證: ![]() ≌△CBE;②DE=AD+BE;
≌△CBE;②DE=AD+BE;
![]() 當直線MN繞點C旋轉到圖2的位置時,
當直線MN繞點C旋轉到圖2的位置時,![]() 中的結論還成立嗎?若成立,請給出證明;若不成立,說明理由.
中的結論還成立嗎?若成立,請給出證明;若不成立,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=x2+bx+c與x軸交于A、B兩點,B點坐標為(4,0),與y軸交于點C(0,4).
(1)求拋物線的解析式;
(2)點P在x軸下方的拋物線上,過點P的直線y=x+m與直線BC交于點E,與y軸交于點F,求PE+EF的最大值;
(3)點D為拋物線對稱軸上一點.
①當△BCD是以BC為直角邊的直角三角形時,直接寫出點D的坐標;
②若△BCD是銳角三角形,直接寫出點D的縱坐標n的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車從A地出發,勻速駛向B地.甲車以80km/h的速度行駛1h后,乙車才沿相同路線行駛.乙車先到達B地并停留1h后,再以原速按原路返回,直至與甲車相遇.在此過程中,兩車之間的距離y(km)與乙車行駛時間x(h)之間的函數關系如圖所示.下列說法:①乙車的速度是120km/h;②m=160;③點H的坐標是(7,80);④n=7.5.其中說法正確的有( )

A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 圖象的頂點為
圖象的頂點為![]() ,其圖象與
,其圖象與![]() 軸的交點
軸的交點![]() 、
、![]() 的橫坐標分別為
的橫坐標分別為![]() ,
,![]() .與
.與![]() 軸負半軸交于點
軸負半軸交于點![]() ,在下面五個結論中:
,在下面五個結論中:
①![]() ;②
;②![]() ;③
;③![]() ;④只有當
;④只有當![]() 時,
時,![]() 是等腰直角三角形;⑤使
是等腰直角三角形;⑤使![]() 為等腰三角形的
為等腰三角形的![]() 值可以有四個.
值可以有四個.
其中正確的結論有( )

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,直線AB交y軸于A(0,a),交x軸于B(b,0),且a,b滿足(a﹣b)2+|3a+5b﹣88|=0.
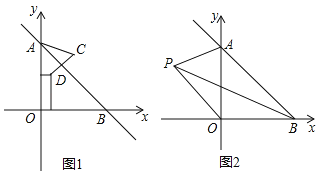
(1)求點A,B的坐標;
(2)如圖1,已知點D(2,5),求點D關于直線AB對稱的點C的坐標.
(3)如圖2,若P是∠OBA的角平分線上的一點,∠APO=67.5°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,橫、縱坐標都是整數的點叫作整點,直線y=kx-3(k>0),與坐標軸圍成的三角形內部(不包含邊界)有且只有三個整點,則k的取值范圍是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,在邊長為
,在邊長為![]() 的小正方形組成的網格中,
的小正方形組成的網格中,![]() 的頂點
的頂點![]() 、
、![]() 均在格點上,點
均在格點上,點![]() 在
在![]() 軸上,點
軸上,點![]() 的坐標為
的坐標為![]() .
.

![]() 點
點![]() 關于點
關于點![]() 中心對稱的點的坐標為________;
中心對稱的點的坐標為________;
![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 后得到
后得到![]() ,那么點
,那么點![]() 的坐標為________;線段
的坐標為________;線段![]() 在旋轉過程中所掃過的面積是________.
在旋轉過程中所掃過的面積是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com