
【題目】(1)如圖,AC平分∠DAB,∠1=∠2,試說明AB與CD的位置關系,并予以證明;
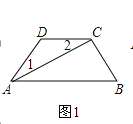
(2)如圖,AB∥CD,AB的下方兩點E、F滿足:BF平分∠ABE、DF平分∠CDE,若∠DFB=20°,∠CDE=70°,求∠ABE的度數;
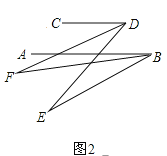
(3)在前面的條件下,若P是BE上一點,G是CD上任一點,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列結論:①∠DGP-∠MGN的值不變;②∠MGN的度數不變,可以證明只有一個是正確的,請你作出正確的選擇并求值.

【答案】(1)AB∥CD;(2)∠ABE=30°;(3)②∠MGN的度數為15°不變,證明見解析.
【解析】
(1)根據內錯角相等,兩直線平行證明即可;
(2)先由角平分線的定義可得:∠CDF=![]() ∠CDE=35°,∠ABE=2∠ABF,然后根據兩直線平行內錯角相等,可得:∠2=∠CDF=35°,然后利用三角形外角的性質求出∠ABF的度數,進而可求∠ABE的度數;
∠CDE=35°,∠ABE=2∠ABF,然后根據兩直線平行內錯角相等,可得:∠2=∠CDF=35°,然后利用三角形外角的性質求出∠ABF的度數,進而可求∠ABE的度數;
(3)根據三角形的一個外角等于與它不相鄰的兩個內角的和可得∠1=∠BPG+∠B,再根據平行線的性質以及角平分線的定義表示出∠MGP、∠DPQ,根據兩直線平行,內錯角相等可得∠NGP=∠GPQ,然后列式表示出∠MGN=![]() ∠B,從而判定②正確.
∠B,從而判定②正確.
(1)結論:AB∥CD.
證明:∵AC平分∠DAB,
∴∠1=∠CAB,
∵∠1=∠2,
∴∠2=∠CAB,
∴AB∥CD;
(2)解:如圖2,
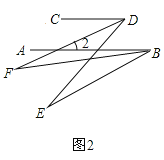
∵BF平分∠ABE,DF平分∠CDE,
∴∠CDF=![]() ∠CDE=35°,∠ABE=2∠ABF,
∠CDE=35°,∠ABE=2∠ABF,
∵CD∥AB,
∴∠2=∠CDF=35°,
∵∠2=∠DFB+∠ABF,∠DFB=20°,
∴∠ABF=15°,
∴∠ABE=2∠ABF=30°;
(3)解:②結論MGN的度數為15°不變.
如圖3,根據三角形的外角性質,∠1=∠BPG+∠B,
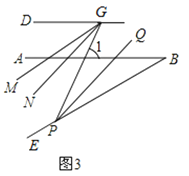
∵PQ平分∠BPG,GM平分∠DGP,
∴∠GPQ=![]() ∠BPG,∠MGP=
∠BPG,∠MGP=![]() ∠DGP,
∠DGP,
∵AB∥CD,
∴∠1=∠DGP,
∴∠MGP=![]() (∠BPG+∠B),
(∠BPG+∠B),
∵PQ∥GN,
∴∠NGP=∠GPQ=![]() ∠BPG,
∠BPG,
∴∠MGN=∠MGP-∠NGP=![]() (∠BPG+∠B)-
(∠BPG+∠B)-![]() ∠BPG=
∠BPG=![]() ∠B,
∠B,
根據前面的條件,∠B=30°,
∴∠MGN=![]() ×30°=15°,
×30°=15°,
∴①∠DGP-∠MGN的值隨∠DGP的變化而變化;②∠MGN的度數為15°不變.


 天天練口算系列答案
天天練口算系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(﹣2,0),B(0,1).
(1)點C的坐標是;
(2)將△ABC沿x軸正方向平移得到△A′B′C′,且B,C兩點的對應點B′,C′恰好落在反比例函數y= ![]() 的圖象上,求該反比例函數的解析式.
的圖象上,求該反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若數a使得關于x的不等式組 ,有且僅有四個整數解,且使關于y的分式方程
,有且僅有四個整數解,且使關于y的分式方程![]() =1有整數解,則所有滿足條件的整數a的值之和是( )
=1有整數解,則所有滿足條件的整數a的值之和是( )
A. 3B. 2C. ﹣2D. ﹣3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(﹣4,n),B(2,﹣4)是一次函數y=kx+b的圖象和反比例函數y=![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1)求反比例函數和一次函數的解析式;
(2)求直線AB與x軸的交點C的坐標及△AOB的面積;
(3)直接寫出一次函數的值小于反比例函數值的x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為增強學生環保意識,某中學組織全校2000名學生參加環保知識大賽,比賽成績均為整數.從中抽取部分同學的成績進行統計,并繪制成如圖統計圖.
請根據圖中提供的信息,解答下列問題:
(1)所抽取的樣本容量為 .
(2)若抽取的學生成績用扇形圖來描述,則表示“第三組(79.5~89.5 )”的扇形的圓心角度數為多少?
(3)如果成績在80分以上(含80分)的同學可以獲獎,請估計該校有多少名同學獲獎.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,過點C的直線MN∥AB,D為AB邊上
一點,過點D作DE⊥BC,交直線MN于E,垂足為F,連接CD,BE.
(1)求證:CE=AD;
(2)當D在AB中點時.
①求證:四邊形BECD是菱形;
②當∠A為多少度時,四邊形BECD是正方形?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①為平地上一幢建筑物與鐵塔圖,圖②為其示意圖.建筑物AB與鐵塔CD都垂直于地面,BD=20m,在A點測得D點的俯角為45°,測得C點的仰角為58°.求鐵塔CD的高度.(參考數據:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)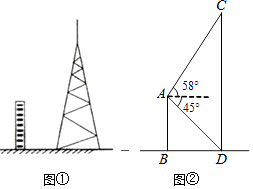
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一個直角三角形紙片ACB,其中∠ACB=90°,AC=4,BC=3,E,F分別是AC,AB邊上點,連接EF,將紙片ACB的一角沿EF折疊.
(1)如圖①,若折疊后點A落在AB邊上的點D處,且使S四邊形ECBF=3S△AEF , 則AE=;
(2)如圖②,若折疊后點A落在BC邊上的點M處,且使MF∥CA.求AE的長;
(3)如圖③,若折疊后點A落在BC延長線上的點N處,且使NF⊥AB.求AE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com