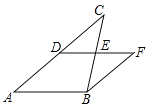
【題目】如圖，DE是△ABC的中位線，延長DE到F，使EF=DE，連接BF
（1）求證：BF=DC；
（2）求證：四邊形ABFD是平行四邊形．
【答案】（1）證明見解析；（2）證明見解析．
【解析】
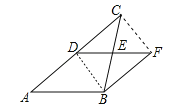
試題分析：（1）連接DB，CF，利用對角線互相平分的四邊形是平行四邊形可得四邊形CDBF是平行四邊形，進(jìn)而可得CD=BF；
（2）由（1）可得CD∥FB，再利用三角形中位線定理可得DF∥AB，根據(jù)兩組對邊分別平行的四邊形是平行四邊形可得結(jié)論．
試題解析：（1）連接DB，CF，∵DE是△ABC的中位線，∴CE=BE，∵EF=ED，∴四邊形CDBF是平行四邊形，∴CD=BF；
（2）∵四邊形CDBF是平行四邊形，∴CD∥FB，∴AD∥BF，∵DE是△ABC的中位線，∴DE∥AB，∴DF∥AB，∴四邊形ABFD是平行四邊形．
科目：初中數(shù)學(xué) 來源： 題型：
【題目】若（x＋m）（x＋n）＝x2-6x＋5，則（ ）
A.m， n同時為負(fù)
B.m，n同時為正；
C.m，n異號
D.m，n異號且絕對值小的為正.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】某市2013年參加中考的考生人數(shù)約為85000人，將85000用科學(xué)記數(shù)法表示為（ ）
A.8.5×104
B.8.5×105
C.0.85×104
D.0.85×105
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】一條防洪堤壩，其橫斷面是梯形，上底寬 
米，下底寬 
米，壩高 
米．
（1）求防洪堤壩的橫斷面積；
（2）如果防洪堤壩長100米，那么這段防洪堤壩的體積是多少立方米？
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，在△ABC 中，AB=20cm，AC=12cm，點 P 從點 B 出發(fā)以每秒 3cm 的速度向點 A 運動，點 Q 從點 A 同時出發(fā)以每秒 2cm 的速度向點 C 運動，其中一個動點到達(dá)端點時，另一個動點也隨之停止運動，當(dāng)△APQ 是以 PQ 為底的等腰三角形時，運動的時間是( )
A.2.5 秒
B.3 秒
C.3.5 秒
D.4 秒
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
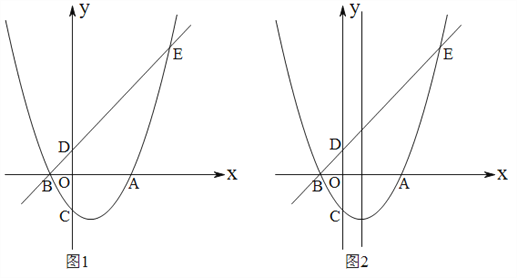
【題目】已知，如圖1：拋物線
交
軸于
、
兩點，交
軸于點
，對稱軸為直線
，且過點
.
（1）求出拋物線的解析式及
點坐標(biāo)，
（2）點
， 
，作直線
交拋物線于另一點
，點
是直線
下方拋物線上的點，連接
、
，求
的面積的最大值，并求出此時點
的坐標(biāo)；
（3）點
、
是拋物線對稱軸上的兩點，且已知
（
， 
），
（
， 
），當(dāng)
為何值時，四邊形
周長最小？并求出四邊形
周長的最小值，請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
