【題目】正方形網(wǎng)格中的交點，我們稱之為格點．如圖所示的網(wǎng)格圖中，每個小正方形的邊長都為
．現(xiàn)有格點
,那么,在網(wǎng)格圖中找出格點
,使以和格點為頂點的三角形的面積為
．這樣的點可找到的個數(shù)為（ ）
A.
B.
C.
D.
【答案】C
【解析】
因為每個小正方形的邊長是1，則可以先找到一點C，則三角形ABC的面積是2，滿足題目要求，再過C點作AB的平行線，平行線與網(wǎng)格點重合的點，因這些點與A、B組成的三角形都是同底等高，則這些三角形的面積都是2，所以這些點即為符合要求的點；同理，過D點作AB的平行線，與網(wǎng)格點重合的點也是符合要求的格點．將所有的符合要求的格點數(shù)加起來，就是問題的答案．
解：如圖所示，在網(wǎng)格圖中可以找到點C，
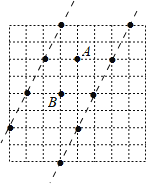
則三角形ABC的面積是2，再過C點作AB的平行線，平行線與網(wǎng)格點重合的點即為符合要求的點，這樣的點有5個；
同樣的方法，過D點作AB的平行線，又能得到4個不同符合要求的格點，
所以符合要求的格點共有：5+4=9（個）；
故選：C．
直通貴州名校周測月考直通名校系列答案科目：初中數(shù)學 來源： 題型：
【題目】a是不為1的有理數(shù)，我們把
稱為a的差倒數(shù)．如:2的差倒數(shù)是
，現(xiàn)已知a1=
，a2是a1的差倒數(shù)，a3是a2的差倒數(shù)，a4是a3的差倒數(shù)，…
(1)求a2，a3，a4的值；
(2)根據(jù)(1)的計算結(jié)果，請猜想并寫出a2016a2017a2018的值；
(3)計算：a33+a66+a99+…+a9999的值．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，在△ABC中，AB＝30 cm，BC＝35 cm，∠B＝60°，有一動點M自A向B以1 cm/s的速度運動，動點N自B向C以2 cm/s的速度運動，若M，N同時分別從A，B出發(fā)．
(1)經(jīng)過多少秒，△BMN為等邊三角形；
(2)經(jīng)過多少秒，△BMN為直角三角形．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖：將ABCD的邊DC延長到點E，使CE=DC，連接AE，交BC于點F， 
（1）求證：△ABF≌△ECF；
（2）若AE=AD，連接AC、BE，求證：四邊形ABEC是矩形．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
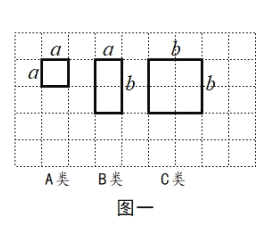
【題目】如圖一，現(xiàn)有足夠多的邊長為
的小正方形紙片(
類)、長為
寬為的長方形紙片(
類)以及邊長為的大正方形紙片(
類)．
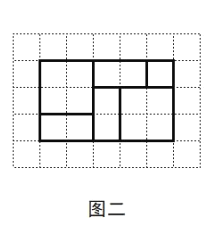
如圖二，小明利用上述三種紙片各若干張，拼出了一個長為
，寬為
的長方形，并用這個長方形解釋了等式
是成立的．
（1）若取圖一中的紙片若干張(三種都要取到)拼成一個長方形(所取紙片用完無剩余)，使它的長和寬分別為
，請你通過計算說明需要類卡片多少張；
（2）若取類紙片
張，類紙片
張，類紙片張，能拼成一個長方形嗎(所取紙片用完無剩余)？請你在圖三中畫出示意圖并在下面直接寫出能用該長方形來解釋成立的等式；
（3）如圖四，大正方形的邊長為
，小正方形的邊長為
，用四個完全相同的長方形的長和寬為別為
．請你通過觀察或計算，判斷下列
個式子是否成立，將其中成立的式子的都填寫在橫線上： (直接填寫序號)．
①
；
②
；
③
；
④
．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，在△ABC中，AB=6，AC=8，BC=10，P為邊BC上一動點(且點P不與點B、C重合)，PE⊥AB于E，PF⊥AC于F，M為EF中點.設(shè)AM的長為x，則x的取值范圍是( )
A. 4≥x＞2.4 B. 4≥x≥2.4 C. 4＞x＞2.4 D. 4＞x≥2.4
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖1，方格圖中每個小正方形的邊長為1，點A、B、C都是格點．
（1）畫出△ABC關(guān)于直線MN對稱的△A1B1C1；
（2）直接寫出AA1的長度；
（3）如圖2，A、C是直線MN同側(cè)固定的點，D是直線MN上的一個動點，在直線MN上畫出點D，使AD+DC最小．（保留作圖痕跡）
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
