如圖，一段拋物線y=﹣x（x﹣1）（0≤x≤1）記為m1，它與x軸交點為O、A1，頂點為P1；將m1繞點A1旋轉180°得m2，交x軸于點A2，頂點為P2；將m2繞點A2旋轉180°得m3，交x軸于點A3，頂點為P3，…，如此進行下去，直至得m10，頂點為P10，則P10的
坐標為（ ）．
科目：初中數學 來源： 題型：
二次函數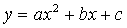
圖象如圖所示，則下列結論正確的（ ）
A．a＞0，b＜0，c＞0 B．a＜0，b＜0，c＞0
C．a＜0，b＞0，c＜0 D．a＜0，b＞0，c＞0
查看答案和解析>>
科目：初中數學 來源： 題型：
把8米長的鋼筋，焊成一個如圖4所示的框架，使其下部為矩形，上部為半圓形.請你寫出鋼筋所焊成框架的面積y(平方米)與半圓的半徑x(米)之間的函數關系式.
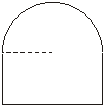
圖4
查看答案和解析>>
科目：初中數學 來源： 題型：
某商場試銷一種成本為60元／件的T恤衫，規定試銷期間銷售單價不低于成本單價，獲利不得高于成本單價的40％．經試銷發現，銷售量y(件)與銷售單價x(元／件)符合一次函數y＝kx＋b，且當x＝70時，y＝50；當x＝80時，y＝40．
(1)求一次函數y=kx＋b的解析式；
(2)若該商場獲得的利潤為w元，試寫出利潤w與銷售單價x之間的關系式；銷售單價定為多少元時，商場可獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，二次函y=ax2+bx+c（a≠0）圖象的一部分，對稱軸為直線x=，且經過點（2，0），下列說法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（﹣2，y1），（，y2）是拋物線上的兩點，則y1＜y2，其中說法正確的是（ ）
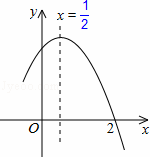
A ①②④ B ③④ C ①③④ D ①②
查看答案和解析>>
科目：初中數學 來源： 題型：
已知拋物線經過A（﹣2，0），B（0，2），C（，0）三點，一動點P從原點出發以1個單位/秒的速度沿x軸正方向運動，連接BP，過點A作直線BP的垂線交y軸于點Q．設點P的運動時間為t秒．
（1）求拋物線的解析式；
（2）當BQ=AP時，求t的值；
（3）隨著點P的運動，拋物線上是否存在一點M，使△MPQ為等邊三角形？若存在，請直接寫t的值及相應點M的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
已知⊙O的半徑為8 cm，A為線段OP的中點，且OP＝16 cm，則點A與⊙O的位置關系是 ( )
A．點A在⊙O內 B．點A在⊙O上
C．點A在⊙O外 D．不能確定
查看答案和解析>>
科目：初中數學 來源： 題型：
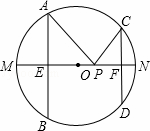
如圖，AB、CD是半徑為5的⊙O的兩條弦，AB=8，CD=6，MN是直徑，AB⊥
MN于點E，CD⊥M
N于點F，P為EF上的任意一點，則PA+PC的最小值為 
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
