
【題目】如圖,△ABC中,∠ACB=90°, CD⊥AB于點D,∠A=30°,BD=1.5cm ,則AB=______cm.

【答案】6
【解析】在直角三角形ABC中,由∠A的度數求出∠B的度數,在直角三角形BCD中,可得出∠BCD度數為30°,根據直角三角形中,30°所對的直角邊等于斜邊的一半,得到BC=2BD,由BD的長求出BC的長,在直角三角形ABC中,同理得到AB=2BC,由BC的長即可求出AB的長.
解:∵△ABC中,∠ACB=90°,∠A=30°,
∴∠B=60°,又CD⊥AB,
∴∠BCD=30°,
在Rt△BCD中,∠BCD=30°,BD=1.5cm,
可得BC=2BD=3cm,
在Rt△ABC中,∠A=30°,BC=3cm,
則AB=2BC=6cm.
故答案為:6.
“點睛”此題考查了含30°角直角三角形的性質,以及三角形的內角和定理,熟練掌握性質是解本題的關鍵.


科目:初中數學 來源: 題型:
【題目】說明命題“若a2>b2,則a>b.”是假命題,舉反例正確的是( )
A. a=2,b=3B. a=﹣2,b=3C. a=3,b=﹣2D. a=﹣3,b=2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各式正確的是( )
A. (a+b)2=a2+b2 B. (x+6)(x﹣6)=x2﹣6
C. (2x+3)2=2x2﹣12x+9 D. (2x﹣1)2=4x2﹣4x+1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣x2+bx+C的圖象過點A(﹣3,0),C(0,3).
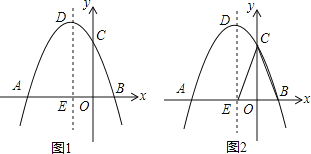
(1)求拋物線的解析式;
(2)探究:在拋物線的對稱軸DE上是否存在點P,使得點P到直線AD和到x軸的距離相等?若存在,求出點P的坐標;若不存在,請說明理由;
(3)探究:在對稱軸DE左側的拋物線上是否存在點F,使得2S△FBC=3S△EBC?若存在,求出點F的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題正確的是( )
A. 有兩個角是直角的四邊形是矩形;
B. 兩條對角線相等的四邊形是矩形;
C. 兩條對角線垂直且相等的四邊形是矩形;
D. 四個角都是直角的四邊形是矩形;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com