【題目】已知關于x的方程x2﹣（2k+1）x+4（k﹣ 
）=0
（1）求證：無論k取何值，這個方程總有實數根；
（2）若等腰三角形ABC的一邊長a=4，另兩邊b、c恰好是這個方程的兩個根，求△ABC的周長．
【答案】
（1）證明：△=（2k+1）2﹣4×4（k﹣ 
）
=4k2+4k+1﹣16k+8，
=4k2﹣12k+9
=（2k﹣3）2，
∵（2k﹣3）2≥0，即△≥0，
∴無論k取何值，這個方程總有實數根
（2）解：當b=c時，△=（2k﹣3）2=0，解得k= 
，方程化為x2﹣4x+4=0，解得b=c=2，而2+2=4，故舍去；
當a=b=4或a=c=4時，把x=4代入方程得16﹣4（2k+1）+4（k﹣ ）=0，解得k= 
，方程化為x2﹣6x+8=0，解得x1=4，x2=2，即a=b=4，c=2或a=c=4，b=2，
所以△ABC的周長=4+4+2=10
【解析】（1）先計算判別式的值得到△=4k2﹣12k+9，配方得到△=（2k﹣3）2 ， 根據非負數的性質易得△≥0，則根據判別式的意義即可得到結論；（2）分類討論：當b=c時，則△=（2k﹣3）2=0，解得k= ，然后解方程得到b=c=2，根據三角形三邊關系可判斷這種情況不符號條件；當a=b=4或a=c=4時，把x=4代入方程可解得k= ，則方程化為x2﹣6x+8=0，解得x1=4，x2=2，所以a=b=4，c=2或a=c=4，b=2，然后計算△ABC的周長．
科目：初中數學 來源： 題型：
【題目】如圖，以圓O為圓心，半徑為1的弧交坐標軸于A，B兩點，P是弧
上一點（不與A，B重合），連接OP，設∠POB=α，則點P的坐標是
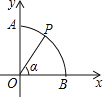
A. （sinα，sinα） B. （cosα，cosα） C. （cosα，sinα） D. （sinα，cosα）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，小明有5張寫著不同數字的卡片，請你按要求抽出卡片，完成下列各題：
（1）若從中抽出2張卡片，且這2個數字的差最小，應如何抽取？最小值是多少？
（2）若從中抽出2張卡片，且這2個數字的積最大，應如何抽取？最小值是多少？
（3）若從中抽出4張卡片，運用加、減、乘、除、乘方、括號等運算符號，使得結果為24.請寫出運算式.（只需寫出一種）
查看答案和解析>>
科目：初中數學 來源： 題型：
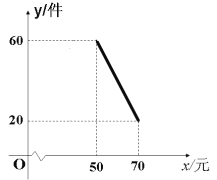
【題目】某商店試銷一種新商品，該商品的進價為40元/件，經過一段時間的試銷發現，每月的銷售量會因售價在40～70元之間的調整而不同。當售價在40～50元時，每月銷售量都為60件；當售價在50～70元時，每月銷售量與售價的關系如圖所示，令每月銷售量為y件，售價為x元/件，每月的總利潤為Q元。
（1）當售價在50～70元時，求每月銷售量為y與x的函數關系式？
（2）當該商品售價x是多少元時，該商店每月獲利最大，最大利潤是多少元？
（3）若該商店每月采購這種新商品的進貨款不低于1760元，則該商品每月最大利潤為 元。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
