
【題目】如圖1,![]() ,
,![]() 是
是![]() 的直徑,點
的直徑,點![]() 在
在![]() 上,連接
上,連接![]() ,
,![]() .
.
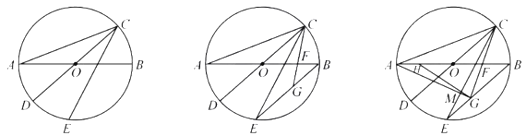
(1)求證:![]() 平分
平分![]() ;
;
(2)如圖2,連接![]() ,點
,點![]() 在
在![]() 上,連接
上,連接![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,點![]() 在
在![]() 上,連接
上,連接![]() ,
,![]() ,
,![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,若
,若![]() ,
,![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)連接![]() ,由
,由![]() ,
,![]() ,
,![]() ,可證明
,可證明![]() ≌
≌![]() ,再根據(jù)全等三角形的性質(zhì),對應(yīng)角相等,即可證明;
,再根據(jù)全等三角形的性質(zhì),對應(yīng)角相等,即可證明;
(2)根據(jù)同弧所對的圓周角相等,可知![]() ,由(1)知
,由(1)知![]() ,得
,得![]() ,又根據(jù)同圓半徑相等,得
,又根據(jù)同圓半徑相等,得![]() ,
,![]() ,由三角形外角等于不相鄰兩內(nèi)角和可得,
,由三角形外角等于不相鄰兩內(nèi)角和可得,![]() ,進而得到
,進而得到![]() ,由此可以證明
,由此可以證明![]() ∥
∥![]() ;
;
(3)過點![]() 作
作![]() ,
,![]() ,
,![]() ,根據(jù)
,根據(jù)![]() ,可知
,可知![]() ,設(shè)
,設(shè)![]() ,
,![]() ,則
,則![]() ,由
,由![]() ,
,![]() ,易知
,易知![]() 為等腰三角形,由
為等腰三角形,由![]() ,可知
,可知![]() ,得AB=10a;再由
,得AB=10a;再由![]() ,可得
,可得![]() ,
,![]() ,再在
,再在![]() 使用勾股定理,可求得
使用勾股定理,可求得![]() ;證明
;證明![]() ≌
≌![]() ,可得
,可得![]() ,解Rt△CPF可得
,解Rt△CPF可得![]() ,則
,則![]() ;由
;由![]() ≌
≌![]() ,
,![]() ,可得
,可得![]() ,
,![]() ;解
;解![]() ,得
,得![]() ,
,![]() ;解等腰
;解等腰![]() 和
和![]() ,得
,得![]() ,再由
,再由![]() 即可求得
即可求得![]() 的值.
的值.
解:(1)如圖,連接![]() ,
,
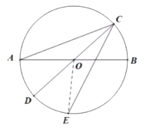
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() ;
;
(2)由(1)知![]() ,
,
∵弧![]() 所對的圓周角相等,
所對的圓周角相等,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∥
∥![]() ;
;
(3)過點![]() 作
作![]() ,
,![]() ,
,![]() ,
,
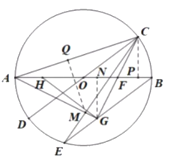
∵![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
設(shè)![]() ,
,![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ∥
∥![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() (舍),
(舍),
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
設(shè)![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:初中數(shù)學(xué) 來源: 題型:
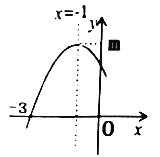
【題目】二次函數(shù)![]() 圖象的一部分如圖所示,頂點坐標為
圖象的一部分如圖所示,頂點坐標為![]() ,與
,與![]() 軸的一個交點的坐標為(-3,0),給出以下結(jié)論:①
軸的一個交點的坐標為(-3,0),給出以下結(jié)論:①![]() ;②
;②![]() ;③若
;③若![]() 、
、![]() 為函數(shù)圖象上的兩點,則
為函數(shù)圖象上的兩點,則![]() ;④當
;④當![]() 時方程
時方程![]() 有實數(shù)根,則
有實數(shù)根,則![]() 的取值范圍是
的取值范圍是![]() .其中正確的結(jié)論的個數(shù)為( )
.其中正確的結(jié)論的個數(shù)為( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
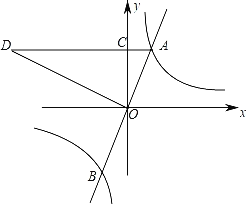
【題目】如圖,直線y1=2x與雙曲線y2=![]() 交于點A,點B,過點A作AC⊥y軸于點C,OC=2,延長AC至D,使CD=4AC,連接OD.
交于點A,點B,過點A作AC⊥y軸于點C,OC=2,延長AC至D,使CD=4AC,連接OD.
(1)求k的值;
(2)求∠AOD的大小;
(3)直接寫出當y1>y2時,x的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
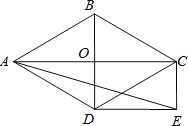
【題目】如圖,菱形ABCD的對角線AC和BD交于點O,分別過點C. D作CE∥BD,DE∥AC,CE和DE交于點E.
(1)求證:四邊形ODEC是矩形;
(2)當∠ADB=60°,AD=2![]() 時,求EA的長。
時,求EA的長。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若拋物線![]() (
(![]() 是常數(shù),
是常數(shù),![]() )與直線
)與直線![]() 都經(jīng)過
都經(jīng)過![]() 軸上的一點
軸上的一點![]() ,且拋物線
,且拋物線![]() 的頂點
的頂點![]() 在直線
在直線![]() 上,則稱此直線
上,則稱此直線![]() 與該拋物線
與該拋物線![]() 具有“一帶一路”關(guān)系.此時,直線
具有“一帶一路”關(guān)系.此時,直線![]() 叫做拋物線
叫做拋物線![]() 的“帶線”,拋物線
的“帶線”,拋物線![]() 叫做直線
叫做直線![]() 的“路線”.
的“路線”.
(1)若直線![]() 與拋物線
與拋物線![]() 具有“一帶一路”關(guān)系,求
具有“一帶一路”關(guān)系,求![]() 的值;
的值;
(2)若某“路線”![]() 的頂點在反比例函數(shù)
的頂點在反比例函數(shù)![]() 的圖象上,它的“帶線”
的圖象上,它的“帶線”![]() 的解析式為
的解析式為![]() ,求此“路線”
,求此“路線”![]() 的解析式;
的解析式;
(3)當常數(shù)![]() 滿足
滿足![]() 時,請直接寫出拋物線
時,請直接寫出拋物線![]() :
:![]() 的“帶線”
的“帶線”![]() 與
與![]() 軸,
軸,![]() 軸所圍成的三角形面積S的取值范圍.
軸所圍成的三角形面積S的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,D為⊙O上一點,點C在直徑BA的延長線上,且∠CDA=∠CBD.
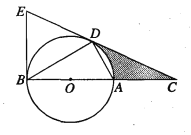
(1)求證:CD是⊙O的切線;
(2)若⊙O的半徑為1,∠CBD=30°,則圖中陰影部分的面積;
(3)過點B作⊙O的切線交CD的延長線于點E若BC=12,tan∠CDA=![]() ,求BE的長.
,求BE的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
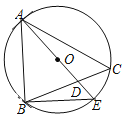
【題目】如圖,在△ABC中,∠C=50°,圓O是△ABC的外接圓,AE為圓O的直徑,AE與BC相交于點D,若AB=AD.則∠EAC=_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】自2020年初新冠肺炎疫情爆發(fā)以來,國內(nèi)經(jīng)濟--度被按下暫停鍵,如今隨著國內(nèi)疫情防控形勢持續(xù)向好,各地開始進人積極復(fù)工復(fù)產(chǎn)的新模式.某商家為降低疫情帶來的影響,刺激消費,吸引顧客,特此設(shè)計了一個游戲,其規(guī)則是:分別轉(zhuǎn)動如圖所示的兩個可以自由轉(zhuǎn)動的轉(zhuǎn)盤各一次,每次指針落在每一字母區(qū)域的機會均等(若指針恰好落在分界線上則重轉(zhuǎn)),當兩個轉(zhuǎn)盤的指針所指字母相同時,消費者就可以獲得一次八折優(yōu)惠價購買商品的機會.
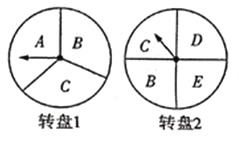
(1)用樹狀圖或列表的方法表示出游戲可能出現(xiàn)的所有結(jié)果;
(2)若小亮參加一次游戲,則他能獲得八折優(yōu)惠價購買商品的概率是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】駱駝被稱為“沙漠之舟”,它的體溫隨時間的變化而發(fā)生較大變化,其體溫(![]() )與時間(小時)之間的關(guān)系如圖1所示.
)與時間(小時)之間的關(guān)系如圖1所示.

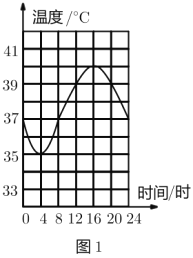
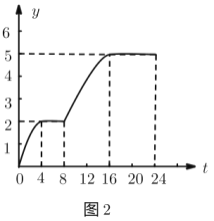
小清同學(xué)根據(jù)圖1繪制了圖2,則圖2中的變量有可能表示的是( ).
A.駱駝在![]() 時刻的體溫與0時體溫的絕對差(即差的絕對值)
時刻的體溫與0時體溫的絕對差(即差的絕對值)
B.駱駝從0時到![]() 時刻之間的最高體溫與當日最低體溫的差
時刻之間的最高體溫與當日最低體溫的差
C.駱駝在![]() 時刻的體溫與當日平均體溫的絕對差
時刻的體溫與當日平均體溫的絕對差
D.駱駝從0時到![]() 時刻之間的體溫最大值與最小值的差
時刻之間的體溫最大值與最小值的差
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com