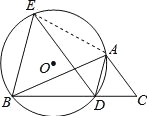
【題目】如圖，已知AD是△ABC的角平分線，⊙O經過A、B、D三點，過點B作BE∥AD，交⊙O于點E，連接ED．
（1）求證：ED∥AC；
（2）連接AE，試證明：ABCD=AEAC．
【答案】(1)證明詳見解析；(2)證明詳見解析.
【解析】
試題分析：（1）由圓周角定理，可得∠BAD=∠E，又由BE∥AD，易證得∠BAD=∠ADE，然后由AD是△ABC的角平分線，證得∠CAD=∠ADE，繼而證得結論；
（2）首先連接AE，易得∠CAD=∠ABE，∠ADC=∠AEB，則可證得△ADC∽△BEA，然后由相似三角形的對應邊成比例，證得結論．
試題解析：（1）∵BE∥AD，
∴∠E=∠ADE，
∵∠BAD=∠E，
∴∠BAD=∠ADE，
∵AD是△ABC的角平分線，
∴∠BAD=∠CAD，
∴∠CAD=∠ADE，
∴ED∥AC；
（2）連接AE，
∵∠CAD=∠ADE，∠ADE=∠ABE，
∴∠CAD=∠ABE，
∵∠ADC+∠ADB=180°，∠ADB+∠AEB=180°，
∴∠ADC=∠AEB，
∴△ADC∽△BEA，
∴AC：AB=CD：AE，
∴ABCD=AEAC．
科目：初中數學 來源： 題型：
【題目】如圖，△ABC內接于⊙O，∠B=60°，CD是⊙O的直徑，點P是CD延長線上一點，且AP=AC．
（1）求證：PA是⊙O的切線；
（2）若PD=1，求⊙O的直徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=
+bx+c的圖象如圖所示，對稱軸為直線x=1．有位學生寫出了以下五個結論：
（1）ac＞0；（2）方程ax2+bx+c=0的兩根是
=﹣1，
=3；（3）2a﹣b=0；（4）當x＞1時，y隨x的增大而減小；則以上結論中正確的有（ ）.
A．1個 B．2個 C．3個 D．4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一次知識競賽共有20道選擇題，規定答對一道得5分，不做或錯一題扣1分，結果某學生得分為88分，則他做對題數為（ ）
A. 16 B. 17 C. 18 D. 19
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD中，AD=CD，∠DAB=∠ACB=90°，過點D作DE⊥AC，垂足為F，DE與AB相交于點E．
（1）求證：ABAF=CBCD；
（2）已知AB=15cm，BC=9cm，P是線段DE上的動點．設DP=x cm，梯形BCDP的面積為y
．
①求y關于x的函數關系式．
②y是否存在最大值？若有求出這個最大值，若不存在請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一次函數y=kx+b﹣x的圖象與x軸的正半軸相交，且函數值y隨自變量x的增大而增大，則k，b的取值情況為（ ）
A.k＞1，b＜0
B.k＞1，b＞0
C.k＞0，b＞0
D.k＞0，b＜0
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，AB是⊙O的直徑，點P在弧AB上（不含點A、B），把△AOP沿OP對折，點A的對應點C恰好落在⊙O上．
（1）當P、C都在AB上方時（如圖1），判斷PO與BC的位置關系（只回答結果）；
（2）當P在AB上方而C在AB下方時（如圖2），（1）中結論還成立嗎？證明你的結論；
（3）當P、C都在AB上方時（如圖3），過C點作CD⊥直線AP于D，且CD是⊙O的切線，證明：AB=4PD．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
