
【題目】如圖,拋物線y=ax2+3x交x軸正半軸于點A(6,0),頂點為M,對稱軸MB交x軸于點B,過點C(2,0)作射線CD交MB于點D(D在x軸上方),OE∥CD交MB于點E,EF∥x軸交CD于點F,作直線MF.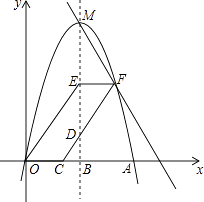
(1)求a的值及M的坐標;
(2)當BD為何值時,點F恰好落在該拋物線上?
(3)當∠DCB=45°時:
①求直線MF的解析式;
②延長OE交FM于點G,四邊形DEGF和四邊形OEDC的面積分別記為S1、S2 , 則S1:S2的值為(直接寫答案)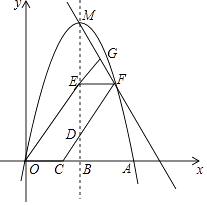
【答案】
(1)解:把A(6,0)代入y=ax2+3x得36a+18=0,解得a=﹣ ![]() ;
;
拋物線解析式為y=﹣ ![]() x2+3x,
x2+3x,
∵y=﹣ ![]() (x﹣3)2+
(x﹣3)2+ ![]() ,
,
∴M點的坐標為(3, ![]() )
)
(2)解:∵CF∥OE,EF∥OC,
∴四邊形OCFE為平行四邊形,
∴EF=OC=2,
∵拋物線的對稱軸為直線x=3,B(3,0),
∴F點的橫坐標為5,
當x=5時,y=﹣ ![]() x2+3x=
x2+3x= ![]() ,即F(5,
,即F(5, ![]() ),
),
∴BE= ![]() ,
,
∵EF∥BC,
∴△BCD∽△EFD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BD= ![]() BE=
BE= ![]() ×
× ![]() =
= ![]() ,
,
即當BD為 ![]() 時,點F恰好落在該拋物線上
時,點F恰好落在該拋物線上
(3)∵CD∥OE,∴∠BOE=∠DCB=45°∴△BOE為等腰直角三角形, ∴BE=OE=3,則E(3,3),∴直線OE的解析式為y=x,同理可得△BCD為等腰直角三角形,∴BD=BC=1,∴DE=2,∵EF∥OC,EF=OC=2,∴F(5,3),設直線MF的解析式為y=kx+b,把M(3,![]() ),F(5,3)代入得
),F(5,3)代入得  ,解得
,解得  ,∴直線MF的解析式為y=﹣
,∴直線MF的解析式為y=﹣ ![]() x+
x+ ![]() ;,
;,![]()
【解析】解:(3)②解方程組  得
得  ,則G(
,則G( ![]() ,
, ![]() ),
),
∴S1=S△GEF+S△DEF= ![]() ×2×(
×2×( ![]() ﹣3)+
﹣3)+ ![]() ×2×2=
×2×2= ![]() ,
,
S2=S△BOE﹣S△BCD= ![]() ×3×3﹣
×3×3﹣ ![]() ×1×1=4,
×1×1=4,
∴ ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
【考點精析】本題主要考查了確定一次函數的表達式和二次函數的最值的相關知識點,需要掌握確定一個一次函數,需要確定一次函數定義式y=kx+b(k不等于0)中的常數k和b.解這類問題的一般方法是待定系數法;如果自變量的取值范圍是全體實數,那么函數在頂點處取得最大值(或最小值),即當x=-b/2a時,y最值=(4ac-b2)/4a才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,tan∠ABC= ![]() ,P為AB上一點,以PB為邊向外作菱形PMNB,連結DM,取DM中點E,連結AE,PE,則
,P為AB上一點,以PB為邊向外作菱形PMNB,連結DM,取DM中點E,連結AE,PE,則 ![]() 的值為( )
的值為( )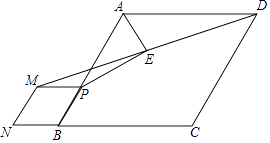
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠A=90°,AB=3,AC=4,D為AC中點,P為AB上的動點,將P繞點D逆時針旋轉90°得到P′,連CP′,則線段CP′的最小值為 . 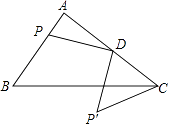
查看答案和解析>>
科目:初中數學 來源: 題型:
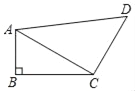
【題目】如圖,四邊形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求證:AC⊥CD;
(2)求四邊形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如下圖時用黑色的正六邊形和白色的正方形按照一定的規律組合而成的兩色圖案

(1)當黑色的正六邊形的塊數為1時,有6塊白色的正方形配套;當黑色的正六邊形塊數為2時,有11塊白色的正方形配套;則當黑色的正六邊形塊數為3,10時,分別寫出白色的正方形配套塊數;
(2)當白色的正方形塊數為201時,求黑色的正六邊形的塊數.
(3)組成白色的正方形的塊數能否為100,如果能,求出黑色的正六邊形的塊數,如果不能,請說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“五一勞動節大酬賓!”,某商場設計的促銷活動如下:在一個不透明的箱子里放有4個相同的小球,球上分別標有“0元”、“10元”、“20元”和“50元”的字樣.規定:在本商場同一日內,顧客每消費滿300元,就可以在箱子里先后摸出兩個球(第一次摸出后不放回).商場根據兩小球所標金額的和返還相等價格的購物券,購物券可以在本商場消費.某顧客剛好消費300元.
(1)該顧客至多可得到元購物券;
(2)請你用畫樹狀圖或列表的方法,求出該顧客所獲得購物券的金額不低于50元的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
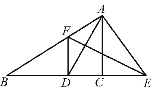
【題目】如圖,在△ABC中,AD是∠BAC的平分線,AD的垂直平分線分別交AB于點F,交BC的延長線于點E.
求證:(1)∠EAD=∠EDA;
(2)DF∥AC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com