
【題目】已知如圖,在數軸上點![]() ,
, ![]() 所對應的數是
所對應的數是![]() ,
, ![]() .
.
對于關于![]() 的代數式
的代數式![]() ,我們規定:當有理數
,我們規定:當有理數![]() 在數軸上所對應的點為
在數軸上所對應的點為![]() 之間(包括點
之間(包括點![]() ,
, ![]() )的任意一點時,代數式
)的任意一點時,代數式![]() 取得所有值的最大值小于等于
取得所有值的最大值小于等于![]() ,最小值大于等于
,最小值大于等于![]() ,則稱代數式
,則稱代數式![]() ,是線段
,是線段![]() 的封閉代數式.
的封閉代數式.
例如,對于關于![]() 的代數式
的代數式![]() ,當
,當![]() 時,代數式
時,代數式![]() 取得最大值是
取得最大值是![]() ;當
;當![]() 時,代數式
時,代數式![]() 取得最小值是
取得最小值是![]() ,所以代數式
,所以代數式![]() 是線段
是線段![]() 的封閉代數式.
的封閉代數式.
問題:(![]() )關于
)關于![]() 代數式
代數式![]() ,當有理數
,當有理數![]() 在數軸上所對應的點為
在數軸上所對應的點為![]() 之間(包括點
之間(包括點![]() ,
, ![]() )的任意一點時,取得的最大值和最小值分別是__________.
)的任意一點時,取得的最大值和最小值分別是__________.
所以代數式![]() __________(填是或不是)線段
__________(填是或不是)線段![]() 的封閉代數式.
的封閉代數式.
(![]() )以下關
)以下關![]() 的代數式:
的代數式:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
是線段![]() 的封閉代數式是__________,并證明(只需要證明是線段
的封閉代數式是__________,并證明(只需要證明是線段![]() 的封閉代數式的式子,不是的不需證明).
的封閉代數式的式子,不是的不需證明).
(![]() )關于
)關于![]() 的代數式
的代數式![]() 是線段
是線段![]() 的封閉代數式,則有理數
的封閉代數式,則有理數![]() 的最大值是__________,最小值是__________.
的最大值是__________,最小值是__________.
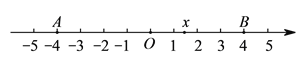
【答案】(![]() )見解析(
)見解析(![]() )④(
)④(![]() )
)![]() ;
; ![]()
【解析】試題分析:(1)觀察數軸,當![]() 時,
時, ![]() 取得最大值為
取得最大值為![]() ,當
,當![]() 時,
時, ![]() 取得最小值為
取得最小值為![]() ,所以代數式
,所以代數式![]() 不是線段
不是線段![]() 的封閉代數式;
的封閉代數式;
(2)按照封閉代數式的定義,逐個分析即可;
(3)觀察代數式可知,當![]() 時,
時, ![]() 取得最大值為
取得最大值為![]() ,列方程求出x的值;當
,列方程求出x的值;當![]() 時,
時,
![]() 取得最小值為
取得最小值為![]() ,列方程求出x的值;然后從中選出最大的和最小的.
,列方程求出x的值;然后從中選出最大的和最小的.
(![]() )解:當
)解:當![]() 時,
時, ![]() 取得最大值為
取得最大值為![]() ,
,
當![]() 時,
時, ![]() 取得最小值為
取得最小值為![]() ,
,
∵![]() 的最大值
的最大值![]() ,
,
∴![]() 不是線段
不是線段![]() 的封閉代數式.
的封閉代數式.
(![]() )證明:①∵
)證明:①∵ ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 的最小值為
的最小值為![]() ,不滿足最小值大于等于
,不滿足最小值大于等于![]() ,
,
∴![]() 不是線段
不是線段![]() 的封閉代數式.
的封閉代數式.
②當![]() 時,
時,
代數式![]() 取得最大值
取得最大值![]() ,不滿足最大值小于等于
,不滿足最大值小于等于![]() ,
,
∴![]() 不是線段
不是線段![]() 的封閉代數式.
的封閉代數式.
③當![]() 時,
時,
代數式![]() 取得最大值
取得最大值![]() ,不滿足最大值小于等于
,不滿足最大值小于等于![]() ,
,
∴![]() 不是線段
不是線段![]() 的封閉代數式.
的封閉代數式.
④當![]() 時,
時,
原式![]()
![]()
![]() ,
,
當![]() 時,
時,
原式![]()
![]()
![]() ,
,
∴![]() ,
,
當![]() 時,
時,
原式![]()
![]()
![]() ,
,
綜上所述: ![]() 滿足最大值小于等于
滿足最大值小于等于![]() ,最小值大于等于
,最小值大于等于![]() ,
,
∴![]() 是線段
是線段![]() 的封閉代數式.
的封閉代數式.
(![]() )當
)當![]() 時,
時,
![]() 取得最大值為
取得最大值為![]() ,
,
則![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
當![]() 時,
時,
![]() 取得最小值為
取得最小值為![]() ,
,
則![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
綜上所述: ![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() .
.
點睛:本題考查了信息遷移類題目的解答,用到了數軸上兩點間的距離,解絕對值方程等知識點和分類討論的數學思想;正確理解“封閉代數式”的意義是解答本題的關鍵.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:初中數學 來源: 題型:
【題目】某農場300名職工耕種51公頃土地,計劃種植水稻,棉花和蔬菜,已知種植農作物每公頃所需的勞動力人數及投入的設備資金如下表:
農作物品種 | 每公頃需勞動力 | 每公頃需投入資金 |
水稻 | 4人 | 1萬元 |
棉花 | 8人 | 1萬元 |
蔬菜 | 5人 | 2萬元 |
已知該農場計劃在設備上投入67萬元,應該怎樣安排三種農作物的種植面積,才能使所有的職工都有工作,而且投入的資金正好夠用?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAC=90°,AB=AC,D點在AC上,E點在BA的延長線上,BD=CE,BD的延長線交CE于F.證明: 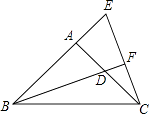
(1)AD=AE
(2)BF⊥CE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區一電瓶小客車接到任務從景區大門出發,向東走2千米到達A景區,繼續向東走2.5千米到達B景區,然后又回頭向西走8.5千米到達C景區,最后回到景區大門.
![]()
(1)以景區大門為原點,向東為正方向,以1個單位長表示1千米,建立如圖所示的數軸,請在數軸上表示出上述A、B、C三個景區的位置.
(2)若電瓶車充足一次電能行走15千米,則該電瓶車能否在一開始充好電而途中不充電的情況下完成此次任務?請計算說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
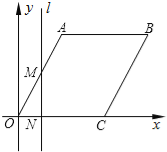
【題目】如圖,在平面直角坐標系中,四邊形OABC是菱形,點C的坐標為(4,0),∠AOC=60°,垂直于x軸的直線l從y軸出發,沿x軸正方向以每秒1個單位長度的速度向右平移,設直線l與菱形OABC的兩邊分別交于點M,N(點M在點N的上方),若△OMN的面積為S,直線l的運動時間為t 秒(0≤t≤4),則能大致反映S與t的函數關系的圖象是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com