
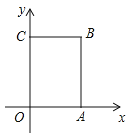
【題目】如圖,在長方形![]() 中,
中,![]() 為平面直角坐標(biāo)系的原點,點
為平面直角坐標(biāo)系的原點,點![]() 的坐標(biāo)分
的坐標(biāo)分![]() ,點
,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點
,點![]() 在第一象限內(nèi),點
在第一象限內(nèi),點![]() 從原點出發(fā),以每秒2個單位長度的速度沿著
從原點出發(fā),以每秒2個單位長度的速度沿著![]() 的路線移動(即沿著長方形移動一周).
的路線移動(即沿著長方形移動一周).
(1)寫出點![]() 的坐標(biāo);
的坐標(biāo);
(2)當(dāng)點![]() 移動了4秒時,求出點
移動了4秒時,求出點![]() 的坐標(biāo).
的坐標(biāo).
(3)在移動過程中,當(dāng)點![]() 到
到![]() 軸的距離為5個單位長度時,求點
軸的距離為5個單位長度時,求點![]() 移動的時間.
移動的時間.
【答案】(1)B(4,6);(2)P(4,4); (3)4.5或7.5.
【解析】
(1)由題意,根據(jù)A與C坐標(biāo)確定出OC與OA的長,即可確定出點B的坐標(biāo);
(2)由P移動的速度與時間確定出移動的路程,求出AP的長,根據(jù)此時P在AB邊上,確定出P的坐標(biāo)即可;
(3)分兩種情況考慮:當(dāng)P在AB邊上;當(dāng)P在OC邊上,分別求出P移動的時間即可.
(1)∵長方形OABC中,O為平面直角坐標(biāo)系的原點,A點的坐標(biāo)為(4,0),C點的坐標(biāo)為(0,6),B在第一象限,
∴OA=BC=4,OC=AB=6,
則B坐標(biāo)為(4,6);
(2)∵P移動的速度為每秒2個單位,且運動時間是4秒,
∴P移動的路程為8個單位,
∴此時P在AB邊上,且AP=4,
則P坐標(biāo)為(4,4);
(3)分兩種情況考慮:
當(dāng)P在AB邊上時,由PA=5,得到P移動的路程為5+4=9,
此時P移動的時間為9÷2=4.5(秒);
當(dāng)P在CO邊上時,由OP=5,得到P移動的路程為4+6+4+1=15,
此時P移動的時間是15÷2=7.5(秒),
綜上,P移動的時間為4.5秒或7.5秒.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:三角形ABC中,∠A=90°,AB=AC,D為BC的中點,
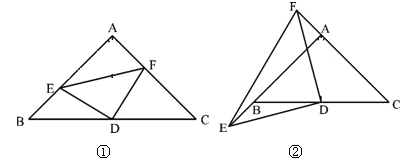
(1)如圖①,E,F分別是AB,AC上的點,且BE=AF,求證:△DEF為等腰直角三角形.
(2)如圖②,若E,F分別為AB,CA延長線上的點,仍有BE=AF,其他條件不變,那么△DEF是否仍為等腰直角三角形?證明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)軸上M、O、N三點對應(yīng)的數(shù)分別為﹣2、0、6,點P為數(shù)軸上任意一點,其對應(yīng)的數(shù)為x.
![]()
(1)求MN的長;
(2)若點P是MN的中點,則x的值是 .
(3)數(shù)軸上是否存在一點P,使點P到點M、N的距離之和是10?若存在,求出x的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為保持水土,美化環(huán)境,W中學(xué)準備在從校門口到柏油公路的這一段土路的兩側(cè)栽一些樹,并要求土路兩側(cè)樹的棵數(shù)相等間距也相等,且首、尾兩端均栽上樹,現(xiàn)在學(xué)校已備好一批樹苗,若間隔30米栽一棵,則缺少22棵;若間隔35米栽一棵,則缺少14棵
(1)求學(xué)校備好的樹苗棵數(shù).
(2)某苗圃負責(zé)人聽說W中學(xué)想在校外土路兩旁栽樹的上述情況后,覺得兩樹間距太大,既不美觀,又影響防風(fēng)固沙的效果,決定無償支援W中學(xué)300棵樹苗.請問,這些樹苗加上學(xué)校自己備好的樹苗,間隔5米栽一棵,是否夠用?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
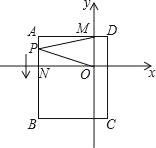
【題目】如圖,平面直角坐標(biāo)系中,ABCD為長方形,其中點A、C坐標(biāo)分別為(﹣8,4)、(2,﹣8),且AD∥x軸,交y軸于M點,AB交x軸于N.
(1)求B、D兩點坐標(biāo)和長方形ABCD的面積;
(2)一動點P從A出發(fā)(不與A點重合),以![]() 個單位/秒的速度沿AB向B點運動,在P點運動過程中,連接MP、OP,請直接寫出∠AMP、∠MPO、∠PON之間的數(shù)量關(guān)系;
個單位/秒的速度沿AB向B點運動,在P點運動過程中,連接MP、OP,請直接寫出∠AMP、∠MPO、∠PON之間的數(shù)量關(guān)系;
(3)是否存在某一時刻t,使三角形AMP的面積等于長方形面積的![]() ?若存在,求t的值并求此時點P的坐標(biāo);若不存在請說明理由.
?若存在,求t的值并求此時點P的坐標(biāo);若不存在請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AC是某市環(huán)城路的一段,AE,BF,CD都是南北方向的街道,其與環(huán)城路AC的交叉路口分別是A,B,C經(jīng)測量東方家具城D位于點A的北偏東45°方向,點B的北偏東30°方向上,AB=2km,∠DAC=15°,求C、D之間的距離(結(jié)果保留根號).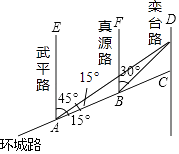
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】先化簡,再求值:
(1)2a+3(a2-b)-2(2a2+a-![]() b),其中a=
b),其中a=![]() ,b=-2;
,b=-2;
(2)(m-5n+4mn)-2(2m-4n+6mn),其中m-n=4,mn=-3.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
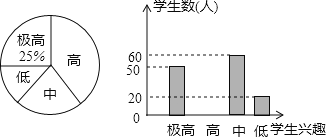
【題目】某中學(xué)為了了解學(xué)生參加體育運動的興趣情況,從全校學(xué)生中隨機抽取部分學(xué)生進行調(diào)查,對樣本數(shù)據(jù)整理后畫出如下統(tǒng)計圖統(tǒng)計圖不夠完整請結(jié)合圖中信息解答下列問題:
![]() 此樣本的樣本容量為:______;
此樣本的樣本容量為:______;
![]() 補全條形統(tǒng)計圖;
補全條形統(tǒng)計圖;
![]() 求興趣為“中”的學(xué)生所占的百分比以及對應(yīng)扇形的圓心角.
求興趣為“中”的學(xué)生所占的百分比以及對應(yīng)扇形的圓心角.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com