
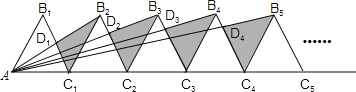
【題目】如圖,n+1個邊長為2的等邊三角形有一條邊在同一直線上,設△B2D1C1的面積為S1,△B3D2C2的面積為S2,…,△Bn+1DnCn的面積為Sn,則S2= ;Sn= .(用含n的式子表示)
【答案】S2=![]() ;Sn=
;Sn=![]() .
.
【解析】
試題分析:由三角形的相似性可求得S2、S3、S4的值,則Sn的值也可用含n的式子表示出來.
解:由于各三角形為等邊三角形,且各邊長為2,過各三角形的頂點B1、B2、B3…向對邊作垂線,垂足為M1、M2、M3,
∵△AB1C1是等邊三角形,
∴AD1=AC1sin60°=2×![]() =
=![]() ,
,
∵△B1C1B2也是等邊三角形,
∴C1B1是∠AC1B2的角平分線,
∴AD1=B2D1=![]() ,
,
故S1=S△B2C1A﹣S△AC1D1=![]() ×2×
×2×![]() ﹣
﹣![]() ×2×
×2×![]() =
=![]() ;
;
S2=S△B3C2A﹣S△AC2D2=![]() ×4×
×4×![]() ﹣
﹣![]() ×4×
×4×![]() =2
=2![]() ﹣
﹣![]() =
=![]() ;
;
作AB∥B1C1,使AB=AB1,連接BB1,則B2,B3,…Bn在一條直線上.
∵Bn Cn∥AB,
∴![]() =
=![]() =
=![]() ,
,
∴BnDn=![]() AB=
AB=![]() ,
,
則DnCn=2﹣BnDn=2﹣![]() =
=![]() .
.
△BnCnBn+1是邊長是2的等邊三角形,因而面積是:![]() .
.
△Bn+1DnCn面積為Sn=![]()
![]() =
=![]()
![]() =
=![]() .
.
即第n個圖形的面積Sn=![]() .
.


科目:初中數學 來源: 題型:
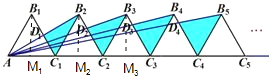
【題目】如圖 1,二次函數![]() 的圖像過點 A (3,0),B (0,4)兩點,動點 P 從 A 出發,在線段 AB 上沿 A → B 的方向以每秒 2 個單位長度的速度運動,過點P作 PD⊥y 于點 D ,交拋物線于點 C .設運動時間為 t (秒).
的圖像過點 A (3,0),B (0,4)兩點,動點 P 從 A 出發,在線段 AB 上沿 A → B 的方向以每秒 2 個單位長度的速度運動,過點P作 PD⊥y 于點 D ,交拋物線于點 C .設運動時間為 t (秒).
(1)求二次函數![]() 的表達式;
的表達式;
(2)連接 BC ,當t=![]() 時,求△BCP的面積;
時,求△BCP的面積;
(3)如圖 2,動點 P 從 A 出發時,動點 Q 同時從 O 出發,在線段 OA 上沿 O→A 的方向以 1個單位長度的速度運動,當點 P 與 B 重合時,P 、 Q 兩點同時停止運動,連接 DQ 、 PQ ,將△DPQ沿直線 PC 折疊到 △DPE .在運動過程中,設 △DPE 和 △OAB重合部分的面積為 S ,直接寫出 S 與 t 的函數關系式及 t 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,BD⊥AD,∠A=45°,E、F分別是AB、CD上的點,且BE=DF,連接EF交BD于O.
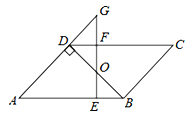
(1)求證:BO=DO;
(2)若EF⊥AB,延長EF交AD的延長線于G,當FG=1時,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
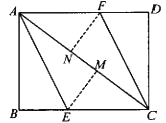
【題目】如圖,AC為矩形ABCD的對角線,將邊AB沿AE折疊,使點B落在AC上的點M處,將邊CD沿CF折疊,使點D落在AC上的點N處。
(1)求證:四邊形AECF是平行四邊形;
(2)若AB=6,AC=10,求四邊形AECF的面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
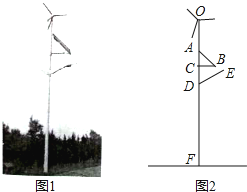
【題目】如圖1,濱海廣場裝有風能、太陽能發電的風光互補環保路燈,燈桿頂端裝有風力發電機,中間裝有太陽能板,下端裝有路燈.該系統工作過程中某一時刻的截面圖如圖2,已知太陽能板的支架BC垂直于燈桿OF,路燈頂端E距離地面6米,DE=1.8米,∠CDE=60°.且根據我市的地理位置設定太陽能板AB的傾斜角為43°.AB=1.5米,CD=1米,為保證長為1米的風力發電機葉片無障礙安全旋轉,對葉片與太陽能板頂端A的最近距離不得少于0.5米,求燈桿OF至少要多高?(利用科學計算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,結果保留兩位小數)
查看答案和解析>>
科目:初中數學 來源: 題型:
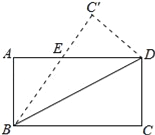
【題目】如圖,在矩形ABCD中,BC=6cm,CD=3cm,將△BCD沿BD翻折,點C落在點C′處,BC′交AD于點E,則AE的長為______ cm.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com