
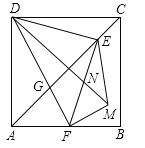
【題目】如圖,正方形ABCD中,AD=4,點E是對角線AC上一點,連接DE,過點E作EF⊥ED,交AB于點F,連接DF,交AC于點G,將△EFG沿EF翻折,得到△EFM,連接DM,交EF于點N,若點F是AB的中點,則△EMN的周長是 .
【答案】![]() .
.
【解析】
試題分析:如圖1,過E作PQ⊥DC,交DC于P,交AB于Q,連接BE,∵DC∥AB,∴PQ⊥AB,∵四邊形ABCD是正方形,∴∠ACD=45°,∴△PEC是等腰直角三角形,∴PE=PC,設PC=x,則PE=x,PD=4﹣x,EQ=4﹣x,∴PD=EQ,∵∠DPE=∠EQF=90°,∠PED=∠EFQ,∴△DPE≌△EQF,∴DE=EF,易證明△DEC≌△BEC,∴DE=BE,∴EF=BE,∵EQ⊥FB,∴FQ=BQ=![]() BF,∵AB=4,F是AB的中點,∴BF=2,∴FQ=BQ=PE=1,∴CE=
BF,∵AB=4,F是AB的中點,∴BF=2,∴FQ=BQ=PE=1,∴CE=![]() ,Rt△DAF中,DF=
,Rt△DAF中,DF=![]() =
=![]() ,∵DE=EF,DE⊥EF,∴△DEF是等腰直角三角形,∴DE=EF=
,∵DE=EF,DE⊥EF,∴△DEF是等腰直角三角形,∴DE=EF=![]() =
=![]() ,∴PD=
,∴PD=![]() =3,如圖2,∵DC∥AB,∴△DGC∽△FGA,∴
=3,如圖2,∵DC∥AB,∴△DGC∽△FGA,∴![]() =
=![]() =2,∴CG=2AG,DG=2FG,∴FG=
=2,∴CG=2AG,DG=2FG,∴FG=![]() =
=![]() ,∵AC=
,∵AC=![]() =
=![]() ,∴CG=
,∴CG=![]() =
=![]() ,∴EG=
,∴EG=![]() =
=![]() ,連接GM、GN,交EF于H,∵∠GFE=45°,∴△GHF是等腰直角三角形,∴GH=FH=
,連接GM、GN,交EF于H,∵∠GFE=45°,∴△GHF是等腰直角三角形,∴GH=FH=![]() =
=![]() ,∴EH=EF﹣FH=
,∴EH=EF﹣FH=![]() ﹣
﹣![]() =
=![]() ,∴∠NDE=∠AEF,∴tan∠NDE=tan∠AEF=
,∴∠NDE=∠AEF,∴tan∠NDE=tan∠AEF=![]() ,∴
,∴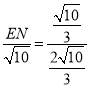 =
=![]() ,∴EN=
,∴EN=![]() ,∴NH=EH﹣EN=
,∴NH=EH﹣EN=![]() ﹣
﹣![]() =
=![]() ,Rt△GNH中,GN=
,Rt△GNH中,GN=![]() =
=![]() =
=![]() ,由折疊得:MN=GN,EM=EG,∴△EMN的周長=EN+MN+EM=
,由折疊得:MN=GN,EM=EG,∴△EMN的周長=EN+MN+EM=![]() +
+![]() +
+![]() =
=![]() ;
;
故答案為:![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
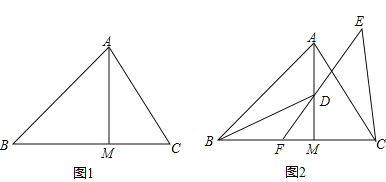
【題目】在△ABC中,∠ABM=45°,AM⊥BM,垂足為M,點C是BM延長線上一點,連接AC.
(1)如圖1,若AB=3![]() ,BC=5,求AC的長;
,BC=5,求AC的長;
(2)如圖2,點D是線段AM上一點,MD=MC,點E是△ABC外一點,EC=AC,連接ED并延長交BC于點F,且點F是線段BC的中點,求證:∠BDF=∠CEF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:探究函數y=|x|﹣2的圖象與性質.
小華根據學習函數的經驗,對函數y=|x|﹣2的圖象與性質進行了探究.
下面是小華的探究過程,請補充完整:
(1)在函數y=|x|﹣2中,自變量x可以是任意實數;
如表是y與x的幾組對應值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m=;
②若A(n,8),B(10,8)為該函數圖象上不同的兩點,則n=;
(2)①如圖,在平面直角坐標系xOy中,描出以上表中各對對應值為坐標的點.并根據描出的點,畫出該函數的圖象;
(3)該函數的最小值為;
(4)已知直線 ![]() 與函數y=|x|﹣2的圖象交于C、D兩點,當y1≥y時x的取值范圍是 .
與函數y=|x|﹣2的圖象交于C、D兩點,當y1≥y時x的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各式由左邊到右邊的變形中,屬于分解因式的是( )
A.a(x+y)=ax+ay
B.x2﹣4x+4=x(x﹣4)+4
C.10x2﹣5x=5x(2x﹣1)
D.x2﹣16+6x=(x+4)(x﹣4)+6x
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題6分)甲、乙兩人進行摸牌游戲.現有三張形狀大小完全相同的牌,正面分別標有數字2,3,5.將三張牌背面朝上,洗勻后放在桌子上.
(1)甲從中隨機抽取一張牌,記錄數字后放回洗勻,乙再隨機抽取一張.請用列表法或畫樹狀圖的方法,求兩人抽取相同數字的概率;
(2)若兩人抽取的數字和為2的倍數,則甲獲勝;若抽取的數字和為5的倍數,則乙獲勝.這個游戲公平嗎?請用概率的知識加以解釋.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com