Question

【題目】中國高鐵迅猛發展，給我們的出行帶來極大的便捷，如圖1，是某種新設計動車車頭的縱截面一部分，曲線OBA是一開口向左，對稱軸正好是水平線OC的拋物線的一部分，點A、B是車頭玻璃罩的最高點和最低點，AC、BD是兩點到車廂底部的距離，OD=1.5米，BD=1.5米，AC=3米，請你利用所學的函數知識解決以下問題．

（1）為了方便研究問題，需要把曲線OBA繞點O旋轉轉化為我們熟悉的函數，請你在所給的方框內，畫出你旋轉后函數圖象的草圖，在圖中標出點O、A、B、C、D對應的位置，并求你所畫的函數的解析式．

（2）如圖2，駕駛員座椅安裝在水平線OC上一點P處，實驗表明：當PA+PB最小時，駕駛員駕駛時視野最佳，為了達到最佳視野，求OP的長．

（3）駕駛員頭頂到玻璃罩的高度至少為0.3米才感到壓抑，一個駕駛員坐下時頭頂到椅面的距離為1米，在（2）的情況下，座椅最多條件到多少時他才感到舒適？

Answer 1

【答案】（1）函數的解析式為y=x2（x≤0）；（2）OP= 3．（3）座椅最多調節得到0.8米時，他才感到舒適．

【解析】試題分析：（1）由圖像的特點知，將曲線OBA繞點O逆時針旋轉90°后變為我們熟悉的二次函數，旋轉后點B的坐標為（﹣1.5，1.5），然后用待定系數法求出解析式；

（2）作點A關于OC的對稱點A′，連結BA′交OC與點P．設DP=x，則PC=4.5﹣x，由

△CA′P∽△DBP列方程求解；

（3）將y=3代入（1）中所求的函數關系式，求出x的值，從而可求出答案.

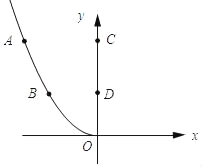
解：（1）將曲線OBA繞點O逆時針旋轉90°如圖所示：則B（﹣1.5，1.5）．

設所畫函數的解析式為y=ax2，將點B的坐標代入得： a=，解得：a=．

∴函數的解析式為y=x2．（x≤0）

（2）如下圖所示：作點A關于OC的對稱點A′，連結BA′交OC與點P．

由（1）可知OC=×32=6，則DC=OC﹣OD=4.5．

∵BD∥CA，

∴△CA′P∽△DBP．

∴=．

設DP=x，則PC=4.5﹣x．

∴=，解得：x=1.5．

∴DP=1.5．

∴OP=OD+DP=3．

（3）將y=3代入y=x2（x≤0），得： x2=3，解得：x=﹣或x=（舍去）．

∴點P到玻璃罩的高度=≈2.1．

∵2.1﹣0.3﹣1=0.8．

∴座椅最多調節得到0.8米時，他才感到舒適．