【題目】△ABC和△DEF中,AB=DE,∠B=∠E,補充條件后仍不一定能保證△ABC≌△DEF,則補充的這個條件為( )
A. BC=EF B. ∠A=∠D C. AC=DF D. ∠C=∠F
優翼小幫手同步口算系列答案科目：初中數學 來源： 題型：
【題目】一個小球從點A（3，3）出發，經過y軸上點C反彈后經過點B（1，0），則小球從A點經過點C到B點經過的最短路線長是（ ）
A．4 B．5 C．6 D．7
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】汽車公司有甲、乙兩種貨車可供租用，現有一批貨物要運往某地，貨主準備租用該公司貨車，已知以往甲、乙兩種貨車運貨情況如下表：
第一次 | 第二次 | |
甲種貨車（輛） | 2 | 5 |
乙種貨車（輛） | 3 | 6 |
累計運貨（噸） | 13 | 28 |
（1）甲、乙兩種貨車每輛可裝多少噸貨物？
（2）若貨主需要租用該公司的甲種貨車8輛，乙種貨車6輛，剛好運完這批貨物，如按每噸付運費50元，則貨主應付運費總額為多少元？
（3）若貨主共有20噸貨，計劃租用該公司的貨車正好（每輛車都滿載）把這批貨運完，該汽車公司共有哪幾種運貨方案？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（Ⅰ）（1）問題引入
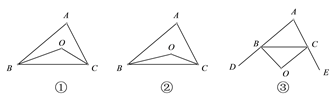
如圖①，在△ABC中，點O是∠ABC和∠ACB平分線的交點，若∠A＝α，則∠BOC＝ （用α表示）；
（2）拓展研究
如圖②，∠CBO＝
∠ABC，∠BCO＝
∠ACB，∠A＝α，試求∠BOC的度數 （用α表示）.（3）歸納猜想
若BO、CO分別是△ABC的∠ABC、∠ACB的n等分線，它們交于點O，∠CBO＝
∠ABC，∠BCO＝
∠ACB，∠A＝α，則∠BOC＝ （用α表示）.
（Ⅱ）類比探索
（1）特例思考
如圖③，∠CBO＝
∠DBC，∠BCO＝
∠ECB，∠A＝α，求∠BOC的度數（用α表示）.
（2）一般猜想
若BO、CO分別是△ABC的外角∠DBC、∠ECB的n等分線，它們交于點O，∠CBO＝
∠DBC，∠BCO＝
∠ECB，∠A＝α，請猜想∠BOC＝ （用α表示）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，把∠B，∠D分別翻折，使點B，D分別落在對角線AC上的點E，F處，折痕分別為CM，AN．
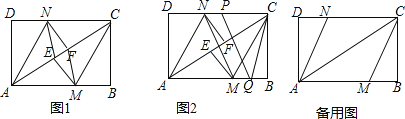
（1）求證：△AND≌△CMB；
（2）連接MF、NE，證明四邊形MFNE是平行四邊形；四邊形MFNE是菱形嗎？請說明理由；
（3）點P、Q是矩形的邊CD、AB上的兩點，連接PQ、CQ、MN，如圖2所示，若PQ=CQ，PQ∥MN，且AB=4，BC=3，DN=
，求PC的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列各式：﹣1+2=1；﹣1+2﹣3+4=2；﹣1+2﹣3+4﹣5+6=3…那么﹣5+6﹣7+8﹣9+10﹣…﹣2015+2016﹣2017+2018=__．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數y=ax2+bx+c的圖象開口向上，對稱軸為直線x=1，圖象經過（3，0），下列結論中，正確的一項是（ ）
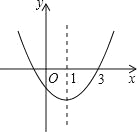
A．4ac﹣b2＜0 B．a﹣b+c＜0 C．2a+b＜0 D．abc＜0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
