
【題目】已知拋物線![]() 與
與![]() 鈾交于
鈾交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,頂點為
,頂點為![]() .
.
(1)求拋物線![]() 的表達式;
的表達式;
(2)若將拋物線![]() 沿
沿![]() 軸平移后得到拋物線
軸平移后得到拋物線![]() ,拋物線
,拋物線![]() 經過點
經過點![]() 且與
且與![]() 軸交于點
軸交于點![]() ,頂點為
,頂點為![]() .在拋物線
.在拋物線![]() 上是否存在一點
上是否存在一點![]() 使
使![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)拋物線![]() 的表達式為
的表達式為![]() ;(2)點
;(2)點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
【解析】
(1)直接利用待定系數(shù)法即可得;
(2)先根據(jù)(1)的結論求出點C、D的坐標,再根據(jù)二次函數(shù)的圖象平移規(guī)律、待定系數(shù)法可求出拋物線![]() 的表達式,從而可得出點
的表達式,從而可得出點![]() 的坐標,然后根據(jù)三角形的面積公式建立等式求解即可得.
的坐標,然后根據(jù)三角形的面積公式建立等式求解即可得.
(1)由題意,將點![]() 代入
代入![]() 得
得![]()
解得![]()
則拋物線![]() 的表達式為
的表達式為![]() ;
;
(2)存在,求解過程如下:
∵![]()
∴![]()
當![]() 時,
時,![]() ,則點C的坐標為
,則點C的坐標為![]()
設拋物線![]() 的表達式為
的表達式為![]()
∵拋物線![]() 經過點
經過點![]()
∴![]() ,解得
,解得![]()
∴拋物線![]() 的表達式為
的表達式為![]()
∴![]()
當![]() 時,
時,![]() ,則點
,則點![]() 的坐標為
的坐標為![]()
∴![]()
設![]()
則在![]() 中,邊
中,邊![]() 上的高為
上的高為![]() ,在
,在![]() 中,邊
中,邊![]() 上的高為
上的高為![]()
∵![]() ,即
,即![]()
∴![]() ,即
,即![]()
解得![]() 或
或![]()
當![]() 時,
時,![]()
當![]() 時,
時,![]()
則點![]() 的坐標為
的坐標為![]() 或
或![]() .
.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數(shù)學 來源: 題型:
【題目】已知如圖,在平面直角坐標系xOy中,點A、B、C分別為坐標軸上上的三個點,且OA=1,OB=3,OC=4,
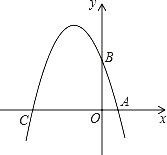
(1)求經過A、B、C三點的拋物線的解析式;
(2)在平面直角坐標系xOy中是否存在一點P,使得以以點A、B、C、P為頂點的四邊形為菱形?若存在,請求出點P的坐標;若不存在,請說明理由;
(3)若點M為該拋物線上一動點,在(2)的條件下,請求出當|PM﹣AM|的最大值時點M的坐標,并直接寫出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,
中,![]() 的頂點
的頂點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 軸的負半軸上,
軸的負半軸上,![]() ,
,![]() 在反比例函數(shù)
在反比例函數(shù)![]() (
(![]() )的圖象上,
)的圖象上,![]() 與
與![]() 軸交于點
軸交于點![]() ,且
,且![]() ,若
,若![]() 的面積是3,則
的面積是3,則![]() 的值是_________.
的值是_________.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,△EBF為等腰直角三角形,點B為直角頂點, 四邊形ABCD是正方形.
⑴ 求證:△ABE≌△CBF;
⑵ CF與AE有什么特殊的位置關系?請證明你的結論.
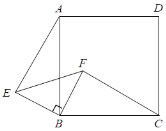
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,已知拋物線![]() 交y軸于點A(0,4),交x軸于點B(4,0)、C,點P是拋物線上一動點,過點P作x軸的垂線PQ,過點A作
交y軸于點A(0,4),交x軸于點B(4,0)、C,點P是拋物線上一動點,過點P作x軸的垂線PQ,過點A作![]() 于點Q,連接AP(AP不平行x軸).
于點Q,連接AP(AP不平行x軸).
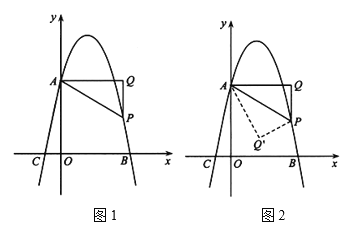
(1)求拋物線的解析式;
(2)點P在拋物線上運動,若![]() ∽
∽![]() (點P與點C對應),求點P的坐標;
(點P與點C對應),求點P的坐標;
(3)如圖2,若點P位于拋物線的對稱軸的右側,將![]() 沿AP對折,點Q的對應點為點
沿AP對折,點Q的對應點為點![]() ,當點
,當點![]() 落在x軸上時,求點P的坐標.
落在x軸上時,求點P的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】疫情無情人有情,愛心捐款傳真情,新型冠狀病毒感染的肺炎疫情期間,某班學生積極參加獻愛心活動,該班50名學生的捐款統(tǒng)計情況如下表:
金額/元 | 5 | 10 | 20 | 50 | 100 |
人數(shù) | 6 | 17 | 14 | 8 | 5 |
則他們捐款金額的眾數(shù)和中位數(shù)分別是( )
A.100,10B.10,20C.17,10D.17,20
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,∠ACB=90°,OC=2OB,tan∠ABC=2,點B的坐標為(1,0).拋物線y=﹣x2+bx+c經過A、B兩點.
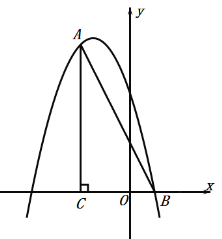
(1)求拋物線的解析式;
(2)點P是直線AB上方拋物線上的一點,過點P作PD垂直x軸于點D,交線段AB于點E,使PE最大.
①求點P的坐標和PE的最大值.
②在直線PD上是否存在點M,使點M在以AB為直徑的圓上;若存在,求出點M的坐標,若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com