
【題目】某校七年級10個班的300名學生即將參加學校舉行的研究旅行活動,學校提出以下4個活動主題:A.赤水丹霞地貌考察;B.平塘天文知識考察;C.山關紅色文化考察;D.海龍電土司文化考察,為了解學生喜歡的活動主題,學生會開展了一次調查研究,請將下面的過程補全
(1)收集數據:學生會計劃調查學生喜歡的活動主題情況,下面抽樣調查的對象選擇合理的是______.(填序號)
①選擇七年級3班、4班、5班學生作為調查對象
②選擇學校旅游攝影社團的學生作為調查對象
③選擇各班學號為6的倍數的學生作為調查對象
(2)整理、描述數據:通過調査后,學生會同學繪制了如下兩幅不完整的統計圖,請把統計圖補充完整
某校七年級學生喜歡的活動主題條形統計圖某校七年級學生喜歡的活動主題扇形統計圖
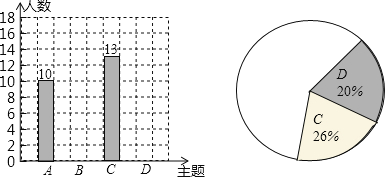
(3)分析數據、推斷結論:請你根據上述調查結果向學校推薦本次活動的主題,你的推薦是______(填A-D的字母代號),估算全年級大約有多少名學生喜歡這個主題活動
(4)若在5名學生會干部(3男2女)中,隨機選取2名同學擔任活動的組長和副組長,求抽出的兩名同學恰好是1男1女的概率.
【答案】(1)③;(2)補全統計圖見解析;(3)B;(4)2名同學恰好是1男1女的概率為![]() .
.
【解析】
(1)根據抽樣調查的代表性求解可得;
(2)先求出被調查的總人數,再乘以D主題對應的百分比求得其人數,繼而根據各主題人數之和等于總人數求得B的人數,然后求出A、B對應的百分比,從而補全圖形;
(3)由統計圖可知選擇的主題,再利用樣本估計總體思想求解可得;
(4)用A表示男生,B表示女生,畫出樹形圖,再根據概率公式進行計算即可.
解:(1)抽樣調查的對象選擇合理的是:③選擇各班學號為6的倍數的學生作為調查對象,故答案為③;
(2)被調查的總人數為13÷26%=50(人),
則D主題人數為50×20%=10(人),B主題人數為50-(10+13+10)=17(人),
∴B主題對應百分比為![]() ×100%=34%,A主題對應的百分比為
×100%=34%,A主題對應的百分比為![]() ×100%=20%,
×100%=20%,
補全統計圖如下:
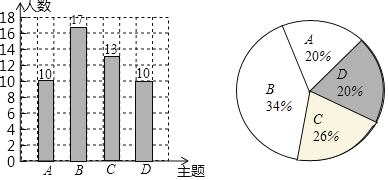
(3)由統計圖知,在所抽取樣本中選擇B主題的人數最多,
所以推薦的主題是B.平塘天文知識考察,
估算全年級喜歡這個主題活動的學生有300×34%=102(人),
故答案為B;
(4)用A表示男生,B表示女生,畫圖如下:

共有20種情況,恰好是1男1女的有12種,
所以2名同學恰好是1男1女的概率為![]() .
.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:初中數學 來源: 題型:
【題目】某交為了開展“陽光體育運動”,計劃購買籃球和足球,已知足球的單價比籃球的單價多![]() 元.若購買
元.若購買![]() 個籃球和
個籃球和![]() 個足球需花費
個足球需花費![]() 元.
元.
(1)求籃球和足球的單價各是多少元;
(2)若學校購買籃球和足球共![]() 個,且購買籃球的總金額不超過購買足球的總金額,則學校最多可購買多少個籃球?
個,且購買籃球的總金額不超過購買足球的總金額,則學校最多可購買多少個籃球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,AC=BC,∠ACB=90°,點D,E分別在AC,BC上,且CD=CE.
(1)如圖1,求證:∠CAE=∠CBD;
(2)如圖2,F是BD的中點,求證:AE⊥CF;
(3)如圖3,F,G分別是BD,AE的中點,若AC=2![]() ,CE=1,求△CGF的面積.
,CE=1,求△CGF的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
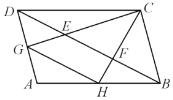
【題目】如圖,![]() ,
,![]() 是平行四邊形
是平行四邊形![]() 從對角線
從對角線![]() 上的兩點,
上的兩點,![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() ,設
,設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,則
,則![]() 與
與![]() 的關系正確的是( )
的關系正確的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=6,BC=8,點E,F分別為邊AD,BC上的一個動點,連接EF,以EF為對稱軸折疊四邊形CDEF,得到四邊形MNFE,點D,C的對應點分別為M,N,當點N恰好落在AB的三等分點時,CF的長為___.
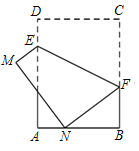
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.為了解一批燈泡的使用壽命,宜采用普查方式
B.擲兩枚質地均勻的硬幣,兩枚硬幣都是正面朝上這一事件發生的概率為![]()
C.擲一枚質地均勻的正方體骰子,骰子停止轉動后,5點朝上是必然事件
D.甲乙兩人在相同條件下各射擊10次,他們成績的平均數相同,方差分別是S甲2=0.4,S乙2=0.6,則甲的射擊成績較穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】劉徵是我國古代最杰出的數學家之一,他在《九算術圓田術)中用“割圓術”證明了圓面積的精確公式,并給出了計算圓周率的科學方法(注:圓周率=圓的周長與該圓直徑的比值)“割圓術”就是以“圓內接正多邊形的面積”,來無限逼近“圓面積”,劉徽形容他的“割圓術”說:割之彌細,所失彌少,割之又割,以至于不可割,則與圓合體,而無所失矣.劉徽計算圓周率是從正六邊形開始的,易知圓的內接正六邊形可分為六個全等的正三角形,每個三角形的邊長均為圓的半徑R.此時圓內接正六邊形的周長為6R,如果將圓內接正六邊形的周長等同于圓的周長,可得圓周率為3.當正十二邊形內接于圓時,如果按照上述方法計算,可得圓周率為_____.(參考數據:sinl5°=0.26)
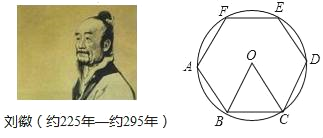
查看答案和解析>>
科目:初中數學 來源: 題型:
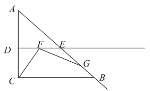
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點,點
的中點,點![]() 為射線
為射線![]() 上一動點,連結
上一動點,連結![]() ,作
,作![]() 交射線
交射線![]() 于點
于點![]() .
.
(1)當點![]() 在線段
在線段![]() 上時,求
上時,求![]() 與
與![]() 的大小關系;
的大小關系;
(2)當![]() 等于多少時,
等于多少時,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com