
【題目】已知:如圖,在梯形ABCD中,AD∥BC,AB=DC,E是對角線AC上一點,且AC·CE=AD·BC.
(1)求證:∠DCA=∠EBC;
(2)延長BE交AD于F,求證:AB2=AF·AD.

 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,點D為拋物線的頂點.
的圖象與x軸交于A、B兩點(點A在點B的左邊),與y軸交于點C,點D為拋物線的頂點.
(1)求A、B、C的坐標;
(2)點M為線段AB上一點(點M不與點A、B重合),過點M作x軸的垂線,與直線AC交于點E,與拋物線交于點P,過點P作PQ∥AB交拋物線于點Q,過點Q作QN⊥x軸于點N.若點P在點Q左邊,當矩形PQMN的周長最大時,求△AEM的面積;
(3)在(2)的條件下,當矩形PMNQ的周長最大時,連接DQ.過拋物線上一點F作y軸的平行線,與直線AC交于點G(點G在點F的上方).若FG=![]() DQ,求點F的坐標.
DQ,求點F的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
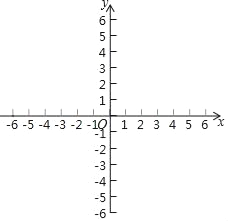
【題目】已知二次函數y=![]() x2﹣x﹣
x2﹣x﹣![]() .
.
(1)在平面直角坐標系內,畫出該二次函數的圖象;
(2)根據圖象寫出:①當x 時,y>0;
②當0<x<4時,y的取值范圍為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
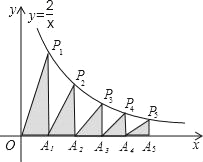
【題目】如圖,在x軸的正半軸上依次截取OA1=A1A2=A2A3=A3A4=A4A5,過點A1、A2、A3、A4、A5分別作x軸的垂線與反比例函數y=![]() (x≠0)的圖象相交于點P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2,A2P3A3,A3P4A4,A4P5A5,并設其面積分別為S1、S2、S3、S4、S5,則S10=_____.(n≥1的整數)
(x≠0)的圖象相交于點P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2,A2P3A3,A3P4A4,A4P5A5,并設其面積分別為S1、S2、S3、S4、S5,則S10=_____.(n≥1的整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:如圖(1),點E、F分別在正方形ABCD的邊BC、CD上,∠EAF=45°,試判斷BE、EF、FD之間的數量關系.
【發現證明】小聰把△ABE繞點A逆時針旋轉90°至△ADG,從而發現EF=BE+FD,請你利用圖(1)證明上述結論.
【類比引申】如圖(2),四邊形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,點E、F分別在邊BC、CD上,則當∠EAF與∠BAD滿足 關系時,仍有EF=BE+FD;請證明你的結論.

【探究應用】如圖(3),在某公園的同一水平面上,四條通道圍成四邊形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分別有景點E、F,且AE⊥AD,DF=40(![]() ﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長.(結果取整數,參考數據:
﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長.(結果取整數,參考數據: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,AC交⊙O于E點,BC交⊙O于D點,CD=BD,∠C=70°.現給出以下四種結論:①∠A=45°;②AC=AB;③AE=BE;④CEAB=2BD2.其中正確結論的序號是( )
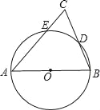
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中數學 來源: 題型:
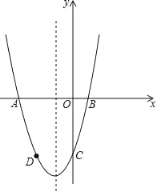
【題目】如圖,已知:二次函數y=x2+bx+c的圖象與x軸交于A,B兩點,其中A點坐標為(﹣3,0),與y軸交于點C,點D(﹣2,﹣3)在拋物線上,
(1)求拋物線的表達式;
(2)拋物線的對稱軸上有一動點P,求出PA+PD的最小值;
(3)若拋物線上有一動點M(點C除外),使△ABM的面積等于△ABC的面積,求M點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,點C在⊙O上(不與A、B重合),∠ACB的平分線交AB于E,交⊙O于D,則下列結論不正確的是( )
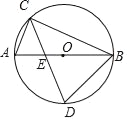
A. AB2=2BD2 B. ACBC=CECD
C. BD2=DEDC D. ACBC+BD2=AB2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題情境)如圖![]() ,
,![]() 中,
中,![]() ,
,![]() ,我們可以利用
,我們可以利用![]() 與
與![]() 相似證明
相似證明![]() ,這個結論我們稱之為射影定理,試證明這個定理;
,這個結論我們稱之為射影定理,試證明這個定理;
(結論運用)如圖![]() ,正方形
,正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() 是對角線
是對角線![]() 、
、![]() 的交點,點
的交點,點![]() 在
在![]() 上,過點
上,過點![]() 作
作![]() ,垂足為
,垂足為![]() ,連接
,連接![]() ,
,
(1)試利用射影定理證明![]() ;
;
(2)若![]() ,求
,求![]() 的長.
的長.
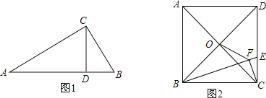
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com