
【題目】如圖,在平面直角坐標系中,直線y=2x+4與x軸交于點A,與y軸交于點B,過點B的直線交x軸于點C,且△ABC面積為10.
(1)求點C的坐標及直線BC的解析式;
(2)如圖1,設點F為線段AB中點,點G為y軸上一動點,連接FG,以FG為邊向FG右側作長形FGQP,且FG:GQ=1:2,在G點的運動過程中,當頂點Q落在直線BC上時,求點G的坐標;
(3)如圖2,若M為線段BC上一點,且滿足S△AMB=S△AOB,點E為直線AM上一動點,在x軸上是存在點D,使以點D,E,B,C為頂點的四邊形為平行四邊形?若存在,請直接寫出點D的坐標;若不在,請說明理由.

【答案】(1)C(3,0),y=﹣![]() x+4;(2)(
x+4;(2)(![]() ,
,![]() );(3)存在,點D的坐標為:(
);(3)存在,點D的坐標為:(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).
【解析】
(1)直線y=2x+4與x軸交于點A,與y軸交于點B,則點A、B的坐標分別為:(﹣2,0)、(0,4),△ABC面積=![]() ×AC×OB=
×AC×OB=![]() AC×4=10,解得:AC=5,故點C(3,0),
AC×4=10,解得:AC=5,故點C(3,0),
將點B、C的坐標代入一次函數表達式,即可求解;
(2)證明△GNQ∽△FMG,則![]() ,即
,即![]() ,故點Q(2m﹣4,m﹣2),即可求解;
,故點Q(2m﹣4,m﹣2),即可求解;
(3)分BC是平行四邊形的邊、BC是平行四邊形的對角線兩種情況,分別求解即可.
解:(1)直線y=2x+4與x軸交于點A,與y軸交于點B,則點A、B的坐標分別為:(﹣2,0)、(0,4),
△ABC面積=![]() ×AC×OB=
×AC×OB=![]() AC×4=10,解得:AC=5,故點C(3,0),
AC×4=10,解得:AC=5,故點C(3,0),
將點B、C的坐標代入一次函數表達式并解得:
直線BC的表達式為:y=﹣![]() x+4…①;
x+4…①;
(2)設點E(m,![]() m+
m+![]() ),點D(n,0),點F為線段AB中點,則點F(﹣1,2),
),點D(n,0),點F為線段AB中點,則點F(﹣1,2),
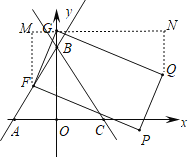
過點G作x軸的平行線MN,過點F、Q分別作y軸的平行線分別交MN于點M、N,
∵∠MGF+∠GFM=90°,∠MGF+∠NGQ=90°,∴∠NGQ=∠GFM,
∠GNQ=∠FMG=90°,
∴△GNQ∽△FMG,
∴![]() ,即
,即![]() ,
,
故:GN=2m﹣4,QN=2,故點Q(2m﹣4,m﹣2),
將點Q的坐標代入y=﹣![]() x+4并解得:m=
x+4并解得:m=![]() ,
,
故點Q(![]() ,
,![]() );
);
(3)S△AMB=S△AOB,則OM∥AB,
則直線OM的表達式為:y=2x…②,
聯立①②并解得:x=![]() ,故點M(
,故點M(![]() ,
,![]() ),
),
同理直線AM的表達式為:y=![]() x+
x+![]() ,
,
設點E(m,![]() m+
m+![]() ),點D(n,0),
),點D(n,0),
①當BC是平行四邊形的邊時,
點B向右平移3個單位向下平移4個單位得到C,
同樣點E(D)向右平移3個單位向下平移4個單位得到D(E),
則m+3=n,![]() m+
m+![]() ﹣4=0或m﹣3=n,
﹣4=0或m﹣3=n,![]() m+
m+![]() +4=0,
+4=0,
解得:n=![]() 或n=﹣
或n=﹣![]() ;
;
②當BC是平行四邊形的對角線時,
由中點公式得:m+n=3,![]() m+
m+![]() +4=0,
+4=0,
解得:n=﹣![]() ,
,
故點D的坐標為:(![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).


 教學練新同步練習系列答案
教學練新同步練習系列答案科目:初中數學 來源: 題型:
【題目】如圖,在離水面高度(AC)為2米的岸上有人用繩子拉船靠岸,開始時繩子與水面的夾角為30°,此人以每秒0.5米的速度收繩子.
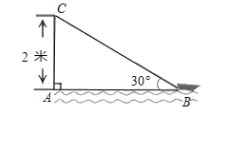
問:(1)未開始收繩子的時候,圖中繩子BC的長度是多少米?
(2)收繩2秒后船離岸邊多少米?(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
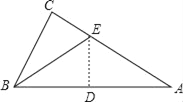
【題目】有一直角三角形紙片,∠C=90°,BC=6,AC=8,現將△ABC按如圖那樣折疊,使點A與點B重合,折痕為DE,則CE的長為( )
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線l:y=kx和拋物線C:y=ax2+bx+1.
(1)當k=1,b=1時,拋物線C:y=ax2+bx+1的頂點在直線l:y=kx上,求a的值;
(2)若把直線l向上平移k2+1個單位長度得到直線r,則無論非零實數k取何值,直線r與拋物線C都只有一個交點;
(i)求此拋物線的解析式;
(ii)若P是此拋物線上任一點,過點P作PQ∥y軸且與直線y=2交于點Q,O為原點,
求證:OP=PQ.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠以每千克200元的價格購進甲種原料360千克,用于生產A、B兩種產品,生產1件A產品或1件B產品所需甲、乙兩種原料的千克數如下表:
產品/原料 | A | B |
甲(千克) | 9 | 4 |
乙(千克) | 3 | 10 |
乙種原料的價格為每千克300元,A產品每件售價3000元,B產品每件售價4200元,現將甲種原料全部用完,設生產A產品x件,B產品m件,公司獲得的總利潤為y元.
(1)寫出m與x的關系式;
(2)求y與x的關系式;
(3)若使用乙種原料不超過510千克,生產A種產品多少件時,公司獲利最大?最大利潤為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在每個邊長都為1的小正方形組成的網格中,點![]() 、
、![]() 、
、![]() 均為格點.
均為格點.
(1)線段![]() 的長度等于______;
的長度等于______;
(2)若![]() 為線段
為線段![]() 上的動點,以
上的動點,以![]() 、
、![]() 為鄰邊的四邊形
為鄰邊的四邊形![]() 為平行四邊形,當
為平行四邊形,當![]() 長度最小時,請你借助網格和無刻度的直尺畫出該平行四邊形,并簡要說明你的作圖方法:__________(不要求證明).
長度最小時,請你借助網格和無刻度的直尺畫出該平行四邊形,并簡要說明你的作圖方法:__________(不要求證明).
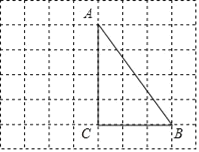
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,O為坐標原點,A(1,1),在x軸上確定點P,使△AOP為等腰三角形,則符合條件的點P的個數共有( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
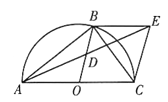
【題目】如圖,![]() 為
為![]() 的直徑,
的直徑,![]() 為
為![]() 上一點,且點
上一點,且點![]() 不與點
不與點![]() 重合,點
重合,點![]() 為半徑
為半徑![]() 的中點,過點
的中點,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() .
.
(1)求證:點![]() 為
為![]() 的中點;
的中點;
(2)連接![]() ,若
,若![]() ,請直接寫出
,請直接寫出![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有五張背面相同的卡片,正面分別印有圓、矩形、等邊三角形、菱形、平行四邊形(鄰邊不相等且不垂直),現將五張卡片正面朝下洗勻任意擺放,從中隨機抽取兩張,抽到的兩張卡片上都恰好印的既是中心對稱又是軸對稱的圖形的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com