【題目】如圖，在平面直角坐標系xOy中，直線AB：y=kx﹣2與y軸相交于點A，與反比例函數y= 
在第一象限內的圖象相交于點B（m，2）． 
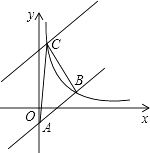
（1）求直線AB的表達式；
（2）將直線AB向上平移后與反比例函數圖象在第一象限內交于點C，且△ABC的面積為18，求平移后的直線的表達式．
【答案】
（1）解：∵點B（m，2）在 
的圖象上，
∴ 
，∴m=4．
∴點B（4，2）．
把點B（4，2）代入y=kx﹣2，
得：4k﹣2=2，
∴k=1．
∴直線AB的表達式為：y=x﹣2
（2）解：設平移后的直線表達式為：y=x+b．
記它與y軸的交點為D，則點D（0，b）．
又 點A（0，﹣2）．
∴AD=b+2．
聯結BD．
∵CD∥AB．
∴S△ABD=S△ABC=18．
即： 
．
∴b=7．
∴平移后的直線表達式為：y=x+7．
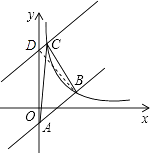
【解析】（1）把B的坐標代入反比例函數的解析式求得B的坐標，然后把B的坐標代入直線解析式，利用待定系數法求得直線AB的解析式；（2）設平移后的直線表達式為：y=x+b，記它與y軸的交點為D，根據CD∥AB可得S△ABD=S△ABC=18，然后利用三角形的面積公式求解．
名師導航單元期末沖刺100分系列答案
名校名卷單元同步訓練測試題系列答案科目：初中數學 來源： 題型：
【題目】下列條件中，不能判定兩個直角三角形全等的是( )
A. 兩個銳角對應相等 B. 一條直角邊和一個銳角對應相等
C. 兩條直角邊對應相等 D. 一條直角邊和一條斜邊對應相等
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某機構對2016年微信用戶的職業頒布進行了隨機抽樣調查（職業說明：A：黨政機關、軍隊，B：事業單位，C：企業，D：自由職業及人體戶，E：學生，F：其他），圖1和圖2是根據調查數據繪制而成的不完整的統計圖.請根據圖中提供的信息，解答下列問題：
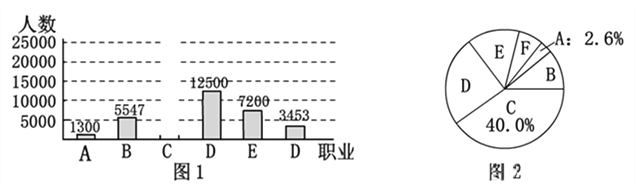
（1）該機構共抽查微信用戶___________人；
（2）在圖.1中，補全條形統計圖；
（3）在圖2中，“D”用戶所對應扇形的圓心角度數為___________度；
(4）2016年微信用戶約有7.5億人，估計“E”用戶大約有________億人.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB=12cm，點C是線段AB上的一點，BC=2AC．動點P從點A出發，以3cm/s的速度向右運動，到達點B后立即返回，以3cm/s的速度向左運動；動點Q從點C出發，以1cm/s的速度向右運動．設它們同時出發，運動時間為ts．當點P與點Q第二次重合時，P、Q兩點停止運動．
（1）AC=__cm，BC=__cm；
（2）當t為何值時，AP=PQ；
（3）當t為何值時，PQ=1cm．
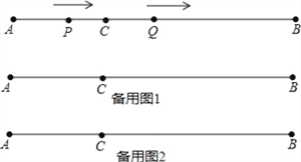
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】規定兩數a，b之間的一種運算，記作(a，b)：如果
，那么(a，b)=c．
例如：因為23=8，所以(2，8)=3．
（1）根據上述規定，填空：
（3，27）=_______，（5，1）=_______，（2，
）=_______．
（2）小明在研究這種運算時發現一個現象：（3n，4n）=（3，4）小明給出了如下的證明：
設（3n，4n）=x，則（3n）x=4n，即（3x）n=4n
所以3x=4，即（3，4）=x，
所以（3n，4n）=（3，4）．
請你嘗試運用這種方法證明下面這個等式：(3，4)+(3，5)=(3，20)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場中，一件夾克衫按成本價提高
后標價，后為了促銷按標價的8折出售，每件240元賣出．
這種夾克衫每件的成本價是多少元？
這種夾克衫的利潤率是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
