Question

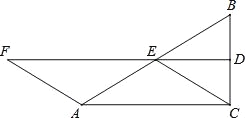
【題目】如圖，△ABC中，∠ACB=90°，D、E分別是BC、BA的中點，連接DE，F在DE延長線上，且AF=AE．

（1）求證：四邊形ACEF是平行四邊形；

（2）若四邊形ACEF是菱形，求∠B的度數．

Answer 1

【答案】（1）證明參見解析；（2）30°．

【解析】

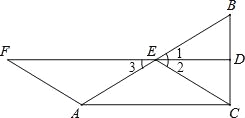
試題分析：（1）如下圖：根據直角三角形斜邊上的中線等于斜邊的一半可得CE=AE=BE，從而得到AF=CE，再根據等腰三角形三線合一的性質可得∠1=∠2，根據等邊對等角可得∠F=∠3，因為∠1=∠3，即可求出∠2=∠F，再根據同位角相等，兩直線平行求出CE∥AF，然后利用一組對邊平行且相等的四邊形是平行四邊形求證；（2）根據菱形的四條邊都相等可得AC=CE，然后求出AC=CE=AE，從而得到△AEC是等邊三角形，再根據等邊三角形的每一個角都是60°求出∠CAE=60°，然后根據直角三角形兩銳角互余解答．

試題解析：（1）∵∠ACB=90°，E是BA的中點，直角三角形斜邊上的中線等于斜邊的一半，∴CE=AE=BE，∵AF=AE，∴AF=CE，在△BEC中，∵BE=CE且D是BC的中點，∴ED是等腰△BEC底邊上的中線，∴ED也是等腰△BEC的頂角平分線，∴∠1=∠2，∵AF=AE，∴∠F=∠3，∵∠1=∠3，∴∠2=∠F，∴CE∥AF，又∵CE=AF，∴四邊形ACEF是平行四邊形（一組對邊平行且相等的四邊形是平行四邊形）；（2）∵四邊形ACEF是菱形，∴AC=CE，由（1）知，AE=CE，∴AC=CE=AE，∴△AEC是等邊三角形，∴∠CAE=60°，在Rt△ABC中，∠B=90°﹣∠CAE=90°﹣60°=30°．故∠B=30°．